모수 (정수)
통계량 (변수)
중심의 경향
◈ 평균
μ
![]()
※
앞으로 ![]() 대신
x
로 표기한다.
대신
x
로 표기한다.
◇ 중위치(median), 최빈치 등이 있으나 거의 사용치 않는다.
산 포
◈ 표준편차
σ
s
실제 관습상, 통계량에서도 σ, σ2 를 사용한다.
◈ 분산
σ2
s2
◈ 편차제곱합
S
「 제곱합 」또는「 변동 」
◇ 범위 (range : R), 4分位數등이 있으나 사용이 적다.
|
제6편 통계 기초 1장 통계 입문 (통계분포, 검정과 추정) |
|
통계의
초심자를 위해 입문에 해당되는 내용을 어느 책보다 쉽게 풀이해보겠다고
이 장을 만들긴합니다만. |
|
|
통계적 방법의 핵심수법인 검정과 추정은 다음과 같은 것들이다.
|
검정 문제의 예시 |
|||||||||||||||||||||||||
|
3) 종전에 어떤 성분의 함량이 0.61% 이었다. 새로운 조건으로 실험한 결과 n = 4 에서 0.53, 0.55, 0.59, 0.65 의 값을 얻었다. 종전과 달라졌다고 할 수 있는가? 4)
25개의 제품에서 4개가 불량이었다. 이 공정은 불량율이 10 % 보다
크다고
볼 수 있는가 ?
|
|
추정 문제의 예시 |
||||||||||||||||||
|
2) 어떤 유기합성에서 반응온도를 80 ℃ 와 70 ℃ 로 각 6회 합성하여 비중을 측정하였더니 다음과 같았다. 양자의 비중의 차는 얼마가 될 것인가?
4) 제품 20 개중에 불량품이 2 개 있다.모 불량율의 95 % 신뢰한계를 구하라. |
통계적 방법은, 관심의 대상이 되는 집단에서 일부(?)를 뽑아 데이터를 만들고 정리하여 옳바른 판단과 결정을 하려는 것이다. 이 때 관심의 대상이 되는 집단 전체를 모집단 (population)이라 하고, 뽑혀진 일부를 표본 (sample)이라 한다.
모집단에 속해있는 개체의 총수 N을 모집단의 크기라고 하며, N이 有限이면 유한모집단, 無限이면 무한모집단 이라 부른다 (공정, 약품의 약효는 무한모집단이다).
표본의 자료로써 모집단의 특성을 알려고 함으로 모집단을 잘 대표하는 샘플을 뽑는 것이 중요하다. 이런 샘플링법에는 주관이 개입되지 않는 제비, 주사위, 난수등을 이용하는 random sampling (무작위 추출법)이 필수적인데, 확률의 이론을 적용할 수 있기 때문이다.
여기서 다시 한번 강조해야 할 사실은, 관측하는 것은 제한된 수의 자료(표본)이나, 우리가 알고자 하거나 조치하려는 것은 그 표본이 속한 모집단이라는 것이다. 표본에 의한 값을 통계량 (statistics)이라 하고, 뽑을 때 마다 값들이 달라지는 변수이며, 모집단의 값들은 모수 (parameter)라 하며 정수(定數)이다. 변수인 통계량으로 모수를 얼마나 잘 맞추느냐가 통계학의 핵심이기도 하다.
일반적으로 통계량은 알파벳, 모수는 그리스 문자로 나타낸다.
|
|
|
모수 (정수) |
통계량 (변수) |
|
|
중심의 경향 |
◈ 평균 |
μ |
|
※
앞으로 |
|
◇ 중위치(median), 최빈치 등이 있으나 거의 사용치 않는다. |
||||
|
산 포 |
◈ 표준편차 |
σ |
s |
실제 관습상, 통계량에서도 σ, σ2 를 사용한다. |
|
◈ 분산 |
σ2 |
s2 |
||
|
◈ 편차제곱합 |
|
S |
「 제곱합 」또는「 변동 」 |
|
|
◇ 범위 (range : R), 4分位數등이 있으나 사용이 적다. |
||||
|
지금
여기에 A조건으로 만든 5개의 데이터가 있다. 동일한 조건으로 만들어진
데이터는 산포가 없다면 이상적으로는 A조건으로 정해지는 값, 즉
모평균 μ 가 될 것이다. 그러나 실제적으로는 그 값 μ 는 모르므로
그 대신 시료의 평균을 모평균 μ 의 추정치(推定値)로 사용한다
|
|
평균
x
= (51 + 48 + 50 + 49 + 52 ) / 5 |
x
= ( x1 + x2
+ x3 + x4
+ x5 ) / n |
그러나 실제의 데이터는 A 조건이라는 영향외에, 우연한 여러가지의 원인으로 같은 값을 나타내지 않는다. 즉 산포가 있다. 이 산포를 계산함에는 모평균 μ 와의 차이로 나타내어야 하나, μ 의 값을 모르므로, 평균치 x 와의 차이를 편차라 하고, vi 로서 나타내자.
|
편차 |
vi |
그러나 편차를 정리하려고 그 합계를 생각하면
|
∑
vi = (1) + (-2) + (0) + (-1) + (2) |
∑
vi = ∑ ( xi - x
) |
언제나
zero가 되어 산포를 나타낼 수가 없다. 그래서 편차를 각각 제곱하고, 그 합계를
구한다. 이를 편차제곱합
( 간단히 제곱합 혹은
변동) 이라고 하며,
S로 나타낸다.
※ 다만 zero를 피하기 위해 제곱하는 것만은 아니다. 데이터가
갖는 정보량으로서 제곱의 값이 타당하다는 설명은 생략한다 (물리법칙에 자주 나타나는
'~의 제곱에 반비례한다' 가 그런 예이다)
|
제곱합
S = (1)2 + (-2)2 + … + (2)2 |
S
= ∑ vi2 = ∑ ( xi
- x
)2 |
윗식은 다음과 같이 변형된다.
|
|
S
= ∑ vi2 = ∑ ( xi
- x
)2 ( ∑ xi )2 / n 를 수정항이라고 하며, CT로 나타낸다. S =
∑ xi 2 - CT |
여기서 편차제곱합 S 는 산포의 '합계' 이므로 평균적인 산포가 필요하게 된다. 즉 데이터의 개수 n 으로 나눈 것을 분산 ( variance : s2 ) 이라 하나, 이렇게 계산된 분산은 모분산을 추정함에 치우침이 있다. 이 치우침을 없애기 위해서 n 대신 ( n - 1 ) 로 나누어야 하는데, 이를 자유도(degree of freedom) 라 한다. 즉 편차제곱합 S 를 자유도 ( n - 1 ) 로 나눈 것을 불편분산 (unbiased variance) V 라 하며, 모분산 ( σ2 )을 치우침없이(不偏) 추정할 수가 있다.
|
σ2 ≡ V = 10 / (5 - 1) = 2.5 |
σ2 ≡ V = S / (n - 1) (※) |
불편분산은 제곱의 형태이므로 측정치와 같은 차원(dimesion)으로 맞추기 위해 제곱근 ( √ ) 한 값을 불편분산의 제곱근 ( √ V ) 이라고 하며, 모표준편차의 추정값으로 사용한다.
|
σ = √ 2.5 |
σ = √ V = √ {S / (n - 1) } (※) |
여기서는 편의상 통계량의 표준편차 s 대신 σ (시그마) 를 사용했다. 일반 현장에서도 그런거와 같이.
◈ 이상은 자다가도 바로 계산할 수 있어야 하는 통계의 ABC 이다. 산포의 이해와 활용없이는 데이터를 바르게 해석할 수 없다. 평균치만으로 조금도 불편함이 없었다고 생각하는 당신이라면 운좋은 지난 날을 자축도 할만 하지만, 더 좋을 수 있었는 날을 놓쳤을지도 모른다.
|
자유도 ( degree of freedom) φ 혹은 f 로 표기 |
|
주어진
조건에서 자유롭게 변화할 수 있는 데이터 수이다. 임의로 5개의
숫자를 선택할 경우 자유도 φ = 5 이다. 그러나 평균이 20
임을 알고 있을 때, 처음 4 개의 수치는 자유롭지만, 5 번째의
수치는 자유롭지못하고 고정값이 된다. 이 때 φ = 4 이다. ( 변동이란
평균과의 차를 문제로 하므로, 이미 평균을 알고 있다는 전제가
있다) |
1.2 정규분포 ( Normal distribution)
화학
천칭(balance)을
써서 동일한 물체를 되풀이 측정하면 그 측정값은 언제나 같은 값이 되지는
않는다. 이것은 측정이 우연적인 여러가지 원인(실험실의 온습도, 측정기의 작동,
기타)에 의하여 좌우되기 때문이다. 그러나 측정값은 제멋대로 나타나는 것은 아니고
참값에 가까운 측정값이 많이 나오고 참값으로 부터 멀리 떨어진 크거나 작은
값은 적을 것이다. 뿐만 아니라 측정오차가 단순한 우연에 지배된다고 하면 참값
보다 큰 쪽과 작은 쪽의 빈도는 거의 같으리라고 짐작된다.
위의 조건 아래서 측정값의
분포는 정규분포(normal
distribution)에 따른다. 같은 성과 나이에서의 키, 같은 공정에서 생산된 부품의
치수나 전구의 효율, 같은 품종의 농작물의 수확량 (이와 같이 측정하는 값들을 계량치라
한다) 등의 히스토그램을 그려보면 정규분포의 형태를 취하고 있음을 알 수 있다.
정규분포의 분포곡선은 종 모양의 대칭곡선이며 plus의 방향과 minus의 방향으로
무한히 뻗쳐져 있다. 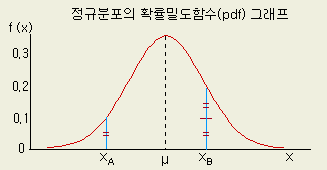
[그림
1-1]
정규분포의 형태
위의
그래프에서 값 xB가 나타날 확률은 값 xA 의 2배가 됨을 나타낸다.
이 곡선(확률밀도함수)의
식은
다음과 같으나 시험칠 일이 없으면 외울 필요가 전혀없다
( 사족 : 그러나
이 홈페이지의 모든 장에서 (※)
표시를 한 식은
사용빈도에서 외워둘만한 식 들이다.
모든 식의 이해가 그렇지만, 그 구성에서
부호는 어떻고 제곱은 어디에 있고 어떤 변수가 어디에 있느냐, 따라서
값이 어떻게 변할것인가 등을 再再 음미하면 식뿐만이 아니라 본문의 이해까지
쉬울 터)
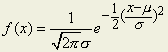
각
문자의 뜻은 다음과 같다.
e…자연대수의 밑(base),
약 2.718
σ…주어진 분포의 표준편차
μ…주어진
분포의 평균
x…가로 좌표(측정 값)
f(x)…세로
좌표 (x값에 대한 곡선의 높이 즉 확률밀도)
정규분포의 표기는 N (평균, 분산) 즉, N ( μ, σ2 )으로 한다.
평균과 표준편차를 달리하는 아래의 정규분포들을 비교해 보라.
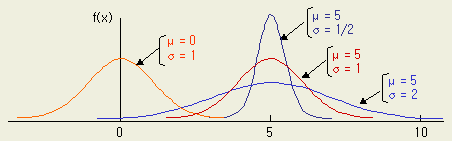
[ 그림 1-2 ] μ 와 σ 에 따른 정규분포의 여러형태
정규분포는
μ 와 σ 에 의해서 결정되며, [그림 1-3 A ] 에 보이는 바와 같이, μ 를 중심으로
±1σ 이내에 68.27 %, ±2σ 이내에는 95.45 %의 확률로 나타나게 된다.
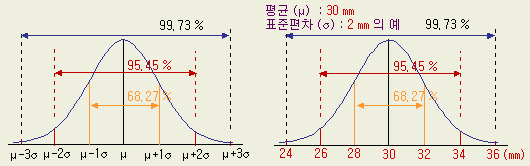
[ 그림 1-3
A ] σ 에 따른 구간내의
비율 [
그림 1-3 B
] μ = 30 ㎜, σ = 2 ㎜ 인 경우
그림
B 는 제품의 길이가 μ
= 30 ㎜, σ = 2 ㎜ 인 경우를 보인다. 26 ㎜ ~ 32 ㎜ 사이는 81.86 % 라는
계산이 나오는가? (대학수능 시험의 평균과 표준편차를 알면 우리집 아들의
전국 석차를 짐작할 수 있다. 단, 수능 시험 성적이 정규분포를 한다는 전제로)
이
넓이가 통계수치표로 만들어져 있으면 편리하겠다. 그러나 [그림 1-2] 에서 보는
바와 같이 평균 μ 와 표준편차 σ 에 따라서 무수한 정규분포가 있으므로 모든 경우를
망라해서 표를 만들 수는 없다. 그러나 우리는 다음과 같은 변환을 하면 어떤 정규분포에
대하여도 적용할 수 있는 방법을 얻게된다.
즉 z
= ( x - μ ) / σ (※)
라는
표준화 변환을 하면, z 는 평균이 0 이고, 분산이 1인 정규분포를 한다. 평균이
0 이고, 분산이 1인 정규분포 N ( 0, 12
)
를 표준정규분포
(standard normal distribution) 라 한다. 식에서 z
란 「 어떤 값 x 가 μ 로 부터 표준편차의 몇배 (몇σ) 떨어져 있는가」를
나타내는 값임에 유의하자.
( 점쟎은 표현으로 '유의하자' 이지 속뜻은 '야무지게
알아두자' 란 의미임을 짐작하실 터)
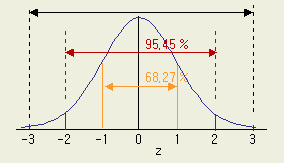
[그림
1-4] 표준화 측도 z 와 넓이 (표준정규분포)
[그림
1-3
B]의 값 34 ㎜ 를 표준화 변환을 하면
z = ( x - μ ) / σ
=
( 34 -30 ) / 2 = 2
즉 34 ㎜란
'평균으로부터 plus 2 σ'
에
있는 값임을 안다. 이 값을 보이는 [그림 1-4] 와 대조해 보라.
이와 같이 모든 정규분포는 표준화 변환을 하면 [그림 1-4] 의 표준정규분포와 match시켜 모집단의 어디에 위치하는가를 알 수 있고 (분포표로써 그 확률까지), 이로써 통계적 확률에 입각한 검추정을 할 수 있게 된다.
표준화된 정규분포에서 ± zσ 內, 또는 ± zσ 外의 주요수치에 대한 확률은 다음표와 같다. 여기서 보이는 z값들은 검추정에서 자주 사용되는 수치들이다.
[표 1-1] 표준화 측도 z 값에 따른 정규분포의 확률
|
z |
|
|
의 미 |
|
0 |
0 |
1.000 |
' |
링크된
확률표의 정규
확률표에는, 임의의
표준측도 z 에 대해서 z 에서 ∞ 에 이르는 표준정규곡선 밑의 넓이(나타날 수 있는
확률)가 주어져 있다. 이것을 누적정규분포표라고 한다. 즉 이 표에 의해서 표준정규분포를
하는 변량의 상대누적도수 (누적%) 를 찾을 수 있다.
표본에 의하여 모집단의 성질을 추측하는 경우 표본에서 계산한 통계량이 바로 모수와 일치한다고는 볼 수 없다. 표본조사가 일부조사이므로 필연적으로 오차가 생긴다. 표본평균 x 는 표본을 뽑을때 마다 달라질 것이다.
지금 표본을 뽑는 실험을 한다. 0 ~ 9 가 각각 1000개씩 있는 다음 표와 같은 모집단을 생각한다.
모집단
분포 
이 경우의 분포곡선은 사각형 형태로, 일양(一樣)분포라 한다.
이 유한모집단 ( N = 10,000 ) 의 평균, 분산 및 표준편차는 각각 다음과 같다.
모평균 μ = 4.5
모분산 σx2 = 8.24 (= 2.872)
모표준편차 σx = 2.87
이 모집단에서 크기가 5 ( n = 5 ) 인 표본을 100회 random sampling 하였다. 이렇게 얻은 표본평균 ( x ) 100 개를 도수분포표로 정리한 것이 [표 1-2 ]의 (1) 란이다.
[표
1-2] 100
회의 표본평균
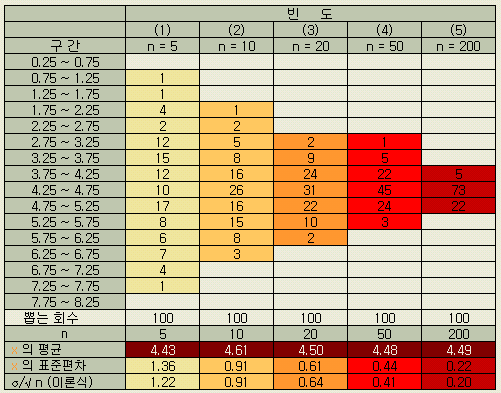
마찬가지로 표본의 크기 n을 10, 20, 50, 200으로 해서 실험한 결과가 각각 (2), (3), (4), (5)난에 적혀 있다. 이 실험에서
①
100
개의 표본평균 ( x
)
들을 다시 평균한 「 x
의 평균 」은 4.43, 4.61, … ,
4.49 로 모평균 μ = 4.50 근방의 값들이다. 만일 뽑는 횟수를 늘려가면 (100 회를
증가시키면) 모평균과의 일치성은 더 좋아지리라 짐작된다.
②
100 개의 표본평균 ( x
)
들의 표준편차는 n 에 커짐에 따라 1.36 에서 0.22 로 점차 작아지고,
x
가
모평균 μ 근방에 집중하고 있다.
③
100 개의 표본평균 ( x
)
의
도수분포를 살펴 보면 모평균에 가까운 x
가
많이 나타나고. 모평균과 떨어질수록 적어진다.
법칙이라고하기에는
좀 뭣하지만 다음과 같은「 大數의
法則 」이 있다.
「
평균 μ 인 모집단에서 크기
n 인 표본을 뽑을 때, n 이 커지면 표본평균 (
x
) 이
점점 모평균
μ 에
가까워진다 」
상식적인 생각으로도, n
이 적을 때는 요행히 몇개가「 분포의 어느 한쪽 귀퉁이 」에서만 연달아 뽑혀져
sample의 평균값이 아주 크거나 작은 값이 될 수도 있지만, n 이 커지면 한쪽
귀퉁이만을 연속적으로 취할 확률은 더욱 적어진다 즉 잘 나타나지 않는다. 즉 랜덤하게
뽑는다면 표본평균 ( x )
은 n 이 커짐에 따라 점점 모평균 μ
로 다가갈 것이다.
위의 표본뽑기의 실험을 통하여, 통계에서 매우 중요한「 中心極限의 定理 」의 개념을 충분히 이해할 수 있으리라 생각한다.
|
「
中心極限의
定理
」-- 활용도가 |
|
모평균이
μ, 모표준편차가
σ 인 모집단에서 크기 n 인 표본을 여러 번 뽑으면 |
|
|
통계에서
정규분포는 그 활용도는 높고
중요하다.
많은
통계값들이 정규분포를 하는 것도 그 이유이지만, 앞에서 본 바와같이 표본평균이라는
중요한 통계량이 (어떤 모집단이라도) 중심극한의 정리에 의해 정규분포로
취급할 수 있기 때문이다.
(통계적 방법에서 자주 이용되는 분포들)
1)
t 분포 --평균치의 해석을 위한
모평균 μ. 분산 σ2 의 정규모집단으로 부터 랜덤하게 취한 n 개의 시료의 평균치 x 의 분포는 모평균 μ, 분산 σ2 / n 인 정규분포를 한다. 또 x 를 표준화하여
z
= ( x
- μ ) / ( σ / √
n )
라 놓으면 z 는 N (0, 12)인 표준정규분포를 한다는 것을 정규분포와
중심극한의 정리에서 알았다.
여기서는 모집단의 표준편차 σ 를 사용하고 있는데, σ 를 모를 경우에는 ( 대부분의 경우가 그렇지만) 다음에서 설명하는 t 분포를 이용해서 평균치의 문제를 해석하게 된다.
σ 대신 그 추정량인 불편분산 V 의 제곱근 √ V 를 대입한 것을 다음과 같은 t0 라 하면
t0
= ( x
- μ ) / ( √
V / √
n ) (※)
단,
√
V = √ {
S / ( n - 1 ) } = √
( S / φ )
이 t0 는 정규분포로 되지 않고, 자유도 φ = n - 1인 t 분포 ( t distribution ) 를 한다. t 분포는 자유도에 따라 형태가 달라지나 좌우대칭이다. φ = ∞ 일 때는 정규분포가 된다.
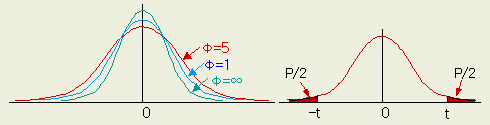
[그림
1- 8] t 분포 [그림
1-9 ] t 분포의 확률
샘플의 사이즈가 작은 현장의 데이터 비교에서 자주 사용된다 . z 와 t0 의 식의 구조를 비교하고 이해를 확실히 하자. 확률표 가기
2) F 분포 --분산의 해석을 위한
동일한
정규모집단 ( ' 분산이 같은 두개의 정규분포 모집단 ' 이라 해도 좋다 ) 에서 취한
크기 n1,
n2
의
두개의 sample 에서 구한 분산을
V1
= S1
/ ( n1
- 1 ) V2
= S2
/ ( n2
- 1 )
로 할 때 V1 과
V2의
비
F0 =
V1 /
V2
라고
하면 이 F0 의
값은 자유도 φ1
= ( n1
- 1 ), φ2
= ( n2
- 1 ) 인 F 분포를 한다. (※)
쉽게 풀어 설명을 하자 ( 고급자는 구질구질한 해설이 되겠지만)
분산이 같은 정규모집단에서, 예로서 n1 = 10 개, n2 = 20 개 두가지의 샘플를 뽑았을 때, 각각에서 계산되는 V1 과 V2 는 비슷할 것으로 예상됨으로 (∵ 본디 분산이 같은 모집단 ) 分散比 F0 = V1 / V2 값은 1주변 (?) 의 값을 가질 것 같기는 하다. ( 모집단 모두를 각각 취한 경우는 F0 = 1.0000000 , 두개의 sample size 가 아주 클 경우는 F0 ≒ 1 이 될 것이다. 역으로 sample size가 아주 작을 경우는 1의 주위라고 할 수 없을 정도로 오락가락하는 것을 조금 뒤에 볼 것이다)
이렇게 계산된 F0 값은 두개의 자유도 φ1 φ2 에 따르는 F 분포(의 법칙)에 따른다. 따라서 역으로 구해진 F0 값이 F 분포도의 어디에 위치하느냐에 따라 두개의 분산이 같으냐, 아니냐를 판단하는 수단이 된다. ( F 분포의 중앙부에 위치한다면 같은 분산이라고 말할 수 있고, 양쪽의 어느 끝에 치우친다면 두개의 분산이 같다고 인정하기가 어려워진다 ) 실험법에서 제일 많이 사용하는 분포법칙이다.
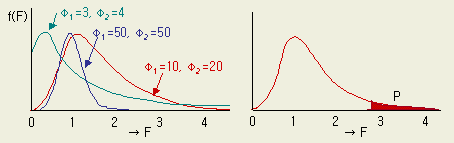
[그림 1-6 ] F 분포 [그림 1- 7] F 분포의 확률
F
분포 곡선은 위의 [그림
1-6]과 같이 분자, 분모의 자유도에
의하여 형태가 결정되며, F0
= 1 가까이에서 極大점이 있다.
분포곡선에서
보는 바와 같이 좌우 대칭이 아니므로, 분포표가 좌 우의 두가지 값을 만들고 비교하여야
하나, F0 =
V1 /
V2
의 계산에서 V1 과
V2
중 큰 값을 분자에 두면, 분포표는 오른쪽의 임계치만 비교하면 되므로
오른쪽의 분포표만으로도 가능하다. 그래서 실제계산에서는 항상 큰 값을 분자에
두고 계산한다. 자유도도 물론 따라간다. ( 단, VB 를 기준으로 VA
를 비교하려는 경우, 분산값의 크고 작음을 떠나 VB 를 분모에 두어야
함은 셈본이다. 다음 장에서 다루는 분산분석에서 항상 오차 분산 Ve
를 분모에 두는 것도 같은 이유에서다. ) 확률표
가기
|
이런 정답지 않는 통계이론을 어떻게 써먹을라는지 ? |
|
측정데이터의 집단을 A, 비교하려는 집단을 B 라고 할 때, A 로
계산된 통계량을 B 분포에 비추어보아, B 의 중앙부(흔히
나타날 수 있는 즉 확률이 높은 곳)에 위치한다면 B 분포와
같다고 해도 문제없을 것이다. 그렇지 않고 분포의 가장자리에 위치한다면
( 여기에서, 대부분의 분포는 양쪽으로 무한히 뻗어져있다는 것을
상기해야 하는 대목이다 ) 분포 B 라고 하기가 어려워진다.
그런데
특성(평균, 산포, 비율등)에 따라 그 분포가 다르다. 그래서 몇가지의
분포법칙을 이해해야 하는 것이다. 이 장의 내용이 약간은 부족할지도
모를 그 최소한이다. 통계의
조예를 깊게하려는 고상한 목표가 아니라,
주먹구구식 판단을 면하기 위함일 뿐이다. |
3)
카이제곱 분포 ( χ2
distribution ) --모분산 및 계수치의 해석을 위한
정규분포
N ( μ, σ2
)의 모집단에서 크기 n 의 샘플을 취하여 계산한
편차제곱합 S 를 모분산 σ2 으로 나누어 X2 (카이제곱) 라는
통계량을 구하면, X2 은 자유도 φ = n - 1 의 카이제곱 ( X2
) 분포를 한다.
X2
= S / σ2
φ = n - 1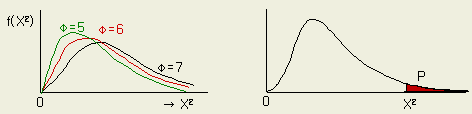
[그림 1-10 ] X2 분포 [그림 1-11 ] X2 분포의 확률
그러므로 어떤 모집단으로 부터 취한 샘플로 계산한 X2 보다 큰 값을 취할 확률을 α 라 하면
X2 (φ ; 1-α/2) < S / σ2 < X2 (φ ; α/2)
라는 값을 S / σ2 이 취할 확률은 (1-α)로 된다.
위의
식을 변형하면
{
S / X2 (φ ; α/2) } > σ2
> { S / X2 (φ
; 1-α/2) }
의 구간에 모분산 σ2 가 있을 확률은 1- α 이다.
계수치의
적합도 검정을 하는 경우
X2 = ∑
{ (실측수 - 기대수)2 / 기대수 }
가
근사적으로 자유도 k - 1 의 카이제곱분포를 한다. ( k 는 그룹의 수) 확률표
가기
어떤
특성에 의하여 모집단을 두 群
(합격과 불합격, 남자와 여자, 찬성과 반대)으로
구분할 수 있는 경우를 베르누이
시행 (Bernoulli trial)
이라 한다. 이런 실험에서 어느 한 사상이 나타나는 횟수의 분포는 이항분포(binomial
distribution) 를 한다.성공의 확률이 p, 실패의 확률이
(1- p)라 하자. 여기서 베르누이 시행을 독립적으로 n 회 반복했을 때
성공횟수가 x 회되는 확률은
P(x)
= (n C x) px
(1- p )n
-x ,
x = 1, 2, …, n
단, (n
C x) = n ! / { x ! (n-x) ! } 즉 n 개에서 x 개를 뽑는 조합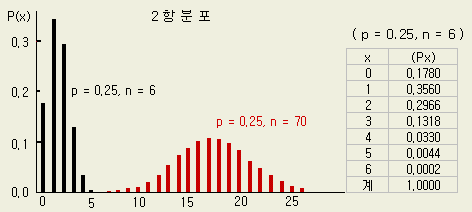
[그림 1-12 ] 2항분포
2항분포의
성질
① 모비율을 P라 할 때, 표본비율 p 의 평균 ( μp
) 과 표준편차 ( σp
) 는
μp
= P
σp
= √
{ P (1-P) / n }
(※)
②
보통 n p ≥ 5 이고, p ≤ 0.5 일 때 에는 정규분포로 취급해도 지장없다.
③
p = 0.5 일때 에는 분포의 형태가 좌우대칭이다.
|
{예제 1} 남·녀 각각 50 % 씩으로 구성된 모집단에서 n = 100명을 뽑을때. 표본에서의 남자의 비율이 0.475 와 0.525 사이에 들어오는 도수 (%) 를 구하라. |
< 풀이 >
P = 0.5 이므로 표본비율 p 의 분포의 중심과 표준편차는 각각
μp
= 0.5
σp
= √ { P (1-P) / n }
=
√ { 0.5 (1- 0.5 ) / 100 } = 0.05
정규분포로 보아,
0.475 와 0.525 를 표준화 하면
(
p - μp
) / σp
= ( 0.475 - 0.5 ) / 0.05 = -0.5
( p - μp
) / σp
= ( 0.525 - 0.5 ) / 0.05 = 0.5
분포표에
의하면 z = -0.5 와 z = +0.5 사이의 넓이는 0.3829 이다.
n 의 값을 크게
하면 p 가 0.475 와 0.525 사이에 들어오는 빈도가 많아진다. 예컨데 n = 400 이면
그 상대빈도(%)는 0.6047 이다.
5) 포아송 분포 (Poisson distribution)
생략
통계적
수법의 핵심으로, 반드시 알아야 하는 내용이 검정과 추정이라 할 것이며 지금까지의
몇가지 통계이론은 이것을 위한 준비학습이다. 이 절과 다음 절에서 검정 및 추정
특히 실험법과 관련한 기본적 사항에 한정해서 작은 volume으로 해설하고자 한다.
설명이 구질구질하다고 느낀다면 귀하의 수준에 자부심을 가질만하고, 이해에 도움된다면
저자의 보람이겠다. 껄끄러운 고비를 여기서도 못넘긴다면, 언제 어디서 넘겠나 (?!)
며 고뇌하자.
|
검정에서의
순서와 방침 |
|
①
문제로 하는 특성(평균, 산포, 불량율 등)에 맞는 통계분포를 고려(선정)하고
|
|
{예제 2} 어떤 공장에서의 약품의 수량(收量)이 종전 74.0 kg 이고, 그 표준편차는 12.0 kg 이었다. 새로운 장치로서 16 회의 제조를 하였던 바 수량의 표준편차는 변하지 않았고 평균은 79.5 kg 이라는 결과가 얻어졌다. 새로운 장치는 수량이 다르다고 할 수 있는가? |
새로운 장치에 의해서 종래의 수량보다 5.5 kg ( = 79.5 - 74.0 ) 만큼 증가하였다고 생각할 수 있으나, 본디 σ = 12.0 kg 의 산포가 있었으므로 종래장치로도 79.5 kg 정도의 수량이 얻어질런지 모른다.
산포를 고려하지 않고, 단지 데이터의 평균이 변하였다고 해서 차가 있다고는 판정하는 것이 '통계에서의 대표적 무식단순'의 표본이다. 그래서 평균치의 문제라도 먼저 산포가 같은지에 대한 검정이 선행되어야 한다. 여기서는 표준편차는 변하지 않았다는 전제가 있으므로 평균치의 검정으로 직행할 수 있다. (산포가 다른 경우라면 좀 복잡한 식을 사용하게 된다)
이 문제는「 새 장치의 모집단 ( 모평균 79.5 kg , 표준편차 12.0 kg) 이 종래의 모집단 ( 모평균 74.0 kg , 표준편차 12.0 kg )과 다른가 ?」이다.
우리는 먼저「 새로운 장치의 수량은 변함없다 」 즉「 79.5 kg 는 모평균 74.0 kg 표준편차 12.0 kg 의 모집단으로부터의 시료이다 」라는 가설(假說)을 세우고, 이 가설을 채택하느냐 기각하느냐를 판정한다.
이런 가설을 귀무가설 ( H0 ) 이라 하며 「 A = B 」라는 형태를 취하고, 이 귀무가설이 기각될 때 채택할 가설도 미리 준비하게 되는데, 이를 대립가설 ( H1 ) 이라 한다. 예를 들면「 A ≠ B 」즉 「 A 와 B 는 같지않다 」든가「 A ≥ B ( 혹은 A ≤ B )」즉「 A 는 B 보다 크다 ( 혹은 작다 )」라는 형태중의 하나가 된다.
|
귀무(歸無)가설을
왜, 어떻게 세우는가? |
|
귀무가설은
보통「 기준 A = 확인하려는 B 」라는 equal (=) 형태로 설정한다.
이렇게 해야만 B의 통계량을, 기준 A 의 통계 법칙에 맞춰보아,
기준 A의 흔하게 나타나는 확률(분포곡선의 중앙부분)에 해당하면
귀무가설이 타당하다는 것이고, 반대로 분포곡선의 양끝부분과
같이 확률적으로 낮은 경우라면, A = B 라고 한 것이 타당하지 못한
것으로 본다. 따라서 귀무가설을 기각하고, 대립가설을 채택하게
된다. |
|
대립가설은 어떻게 세우는가? |
|
귀무가설의
'같다' 에 대립되는 경우는 다음 두가지가 있을 수 있다. 대립가설은 처음에 설정해야 하고, 한쪽검정은 크다 혹은 작다라는 그 분명한 타당성이 있을 때만 설정해야 하며, 그렇지 않으면 양쪽검정으로 해야한다. |
지금의 예에서는 계량치이며, 평균치의 차를 문제로 함으로 정규분포의 응용임을 생각해야 한다. (당연히 문제의 내용에 따라 어떤 분포를 적용할 것인가를 고려하겠지만)
즉 이 경우의 귀무가설
「 한 개의 모집단으로 부터 취한 시료의 평균치이다 」가 성립할 경우를 생각하면, 기준이 되는 종래의 모집단 의 분포곡선은 넓은 폭을 가진 정규분포의 [그림 1-14] ( 그림의 A ) 이 될 것이다. 즉 모집단의 개체 한개 한개 ( x ) 는 분포곡선 A 의 전폭에 걸쳐서 (이론적으로는 왼쪽 0 ~ 오른쪽 ∞) 분포하게 된다. 그리고 이 모집단에서 뽑은 sample size n =16 의 평균치 ( x ) 들은「 中心極限의 定理 」에 의하여 B 와 같은 폭이 좁은 ( 1/ √ n 로 축소) 정규분포를 하게된다.
여기서
B 분포를 알아보면
평균
: 74.0
표준편차
: 12 / √ n = 12 / √
16 = 3.0
즉 N (74.0 , 3.02 ) 이라는 정규분포이다.
여기까지가 기준의 모집단 (종래 장치) 에 대한 분포의 현상이다.
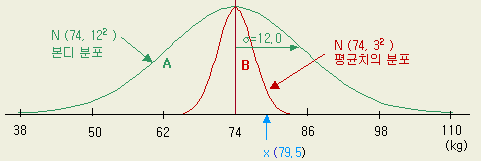
[그림 1-14 ] 종래 표본평균의 분포와 새 장치에 의한 통계량의 접목
지금부터는 비교하려는 모집단 (새 장치)의 데이터를 여기에 접목해본다. 간단히 말해 「 새 장치 = 기존 장치 」라면 새 장치에서의 통계량도 [그림 1-14]와 match 되어야 한다. 즉 새 장치의 평균치 ( x ) 도 [그림 1-14] 의 B 의 분포를 취할 것이다. 그래서 n = 16 의 평균치 79.5 (kg) 을 B 분포에 대입시켜 보게 된다. 그림에서 약간 오른쪽으로 치우쳐 있지만 그런데로 B 분포의 일원 (一員) 이라고 하여 손색 (?) 이 없겠다. ( 눈대중에 의한 이런 표현이 통계를 활용하려는 우리들에게는 ' 말도 되지 않는다는 것' 을 잘 아실 것이다 )
그런데 중요한 사실은 대부분의 분포가 그러하지만 정규분포는 양쪽으로 무한히(!) 뻗어져 있다. 그렇다면 어떤 값이라도 정규분포의 일원이 아니라고는 볼 수 없지 않는가 ? 이러고 보면 판정자체가 불가능하게 된다.
그래서 분포의 끝 ( 나타날 확률이 작은 곳이다 ) 에 좁은 범위를 정하고, 여기에 해당하면 비교하려는 모집단과 다르다고 과감히 짜른다는 것이다.
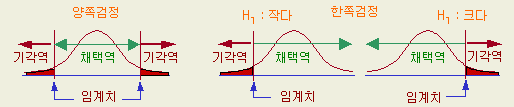
[그림
1-15 ] 양쪽검정과 한쪽검정에서의 채택역과
기각역
그러면
진짜(眞) 같은 한 식구임에도, 단지 키가 너무 크고 작아 귀퉁이에 서게된 죄로 억울하게
판정되는 잘못을 범하지 않는가? 그렇다. 이것은 명백한 판정의 과오이나,
판정이라는 대사(大事)를 위해서는 피할 수 없는 방법이고 위험이다. 여기서 설정하는
작은 부분을 일반적으로 5% 나 1%로 제한하며, 이 값을 有意수준
또는 위험율이라 한다.
여기서
B 분포 (정규분포) 에서의 79.5 를 표준화하여 z 값을 구하면
z0
= ( x - μ ) / σ
=
( 79.5 - 74 ) / 3 = 1.83
정규분포의 양쪽 5 %의 표준화 값은 z (0.05) = 1.96
이므로 한계치 이내의 값이 된다.
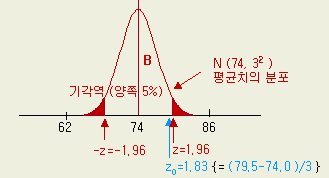
[그림
1-16 ] 새
장치의 통계량의 match
이
예에서는 x
= 79.5 가 분포 B
에서 보는 바와 같이 양쪽의 확률 5 %의 기각역에
들어가지 않으므로 귀무가설을 채택한다. 즉 새 장치의 수량은 종래의 것과
다르다고는 할 수 없다 ('종래의 것과 같다' 고 하지 않음에 유의해야 한다 - 다음의
box 해설 참조)
만약 평균치 ( x )가 5 % 임계치를 넘어 기각역에 해당되면, '유의수준 5 %로 수량은 종전과 다르다' 고 한다. 여기서 유의수준 5 %란 의미는 '이런 식의 결론을 100회 할 때에 최대 5회는 잘못 판단될 수 있다' 는 뜻이다. 유의수준 ( 위험율 ) 을 보통 5 % 와 1 % 를 쓴다고 했는데, ' 과오라면 줄일수록 좋지 않은가 ' 라고 생각할 수 있지만, 이것은 소극적 판단으로 흘러 검정의 의미가 줄어든다. ( 즉 0.0001 %로 한다면 어떤 결과가 될 것인가? 임계치는 매우 넓게 벌어지고, 결국 이것도 저것도 차이가 없다라는 판정으로 흘러, 앞에서 판정자체가 불가능하다는 것과 같은 맥락이다)
검정에서는 항상 유의수준 5 %를 먼저 검정하고, 유의이면 (대립가설을 채택하게 되면) 그 다음으로 다시 유의수준 1 %을 검정하는 순서가 된다.
유의(有意)란
통계적으로 의미가 있다는 뜻이다.「 유의차가 있다 」란 용어는 통계적 검정을 한
후에 사용할 수 있는 단어이다.
|
귀무가설이 채택될 때 ( 판정의 의미와 표현의 아리송함에 대하여) |
|
가설의 검정에서 귀무가설이 채택되어 「 새 장치의 수량은 종래의 것과 다르다고는 할 수 없다 」라고 표현했다. 간단히 「 새 장치의 수량은 종래의 것과 같다」 라고 하지않는 이유는 뭔가 ? 새 장치의 평균 79.5 kg 이라는 것이 실은 위 그림의 C 라는 완전히 다른 모집단의 하나일 수도 있다. 즉 두가지 값의 임계치 사이에 C 와 같은 형태로 걸쳐지는 다른 모집단은 무한히 있을 수 있다. 따라서 평균값이 B 분포의 기각역에 있지않다고 하여「 B 분포( 실은 종전의 장치) 이다」라고 잘라 말할 수는 없게 된다. 따라서 결론의 표현은「 B 이다 혹은 B 와 같다」 가 아니라「 B 가 아니라고는 할 수 없다」가 된다. 귀무가설의 채택이란 엄밀히 말하면 ' 이 정도의 데이터로서는 대립가설 ( = B 가 아니다 )의 채택을 보류한다' 라는 소극적 결론이라고 볼 수 있다. 한편,
임계치를 '벗어'나는 경우는「 유의수준 5 % ( 라는 위험을 무릅쓴다고
했으니 과감하게 )로 종래의 장치와 수량이 다르다 」라는 적극적인
표현이 가능하다. 그것이 어떤 모집단에도 무관하게 |
|
◈
대립가설이 채택될 경우, 검정결과의 표시를 asterisk 의 개수로
간단히 나타내기도 한다. |
한정된 자료로서 모집단에 대한 통계적인 판단을 할 경우 어느 정도의 과오는 불가피하다. 즉 위에서 말한 바와 같이 모집단으로 부터의 시료에 대해서 통계량의 분포를 구하면 임계치를 벗어나는 극히 일어나기 힘든 값일 수가 있다. 그러므로 귀무가설이 옳은데도 불구하고 버리는 수가 있다.
가설이 참(眞)인데 이것을 기각하는 과오를 제1종의 과오라 한다.
이와 반대로 가설이 옳지 않음에도 불구하고 이 확률이 크다는 이유로 가설을 기각하지 않는 경우도 있게 된다. 이러한 과오를 제2종의 과오라 한다. 통계의 문제를 취급하고 있는 이상, 이 두개의 과오를 범하지 않을 수는 없다.
|
통계적 판단의 과오 |
||||||||||||
|
가설검정의 결과를 보면 아래 표와 같은 네가지 경우가 있다.
제1종의 과오를 범할 확률을 α
로 표시하며, 이를 유의수준 (level of
significance) 또는 위험률이라 하고, 제2종의 과오를 범할 확률을
β로
표시하여 ( 1 - β
)의 값을 검출력
(power of test)이라고 한다. 검출력이란 검정하려는 귀무가설이
옳지 않은 경우에 이를 기각(대립가설의 채택)하는 확률이므로 귀무가설의
잘못을 검출해내는 확률이 된다. |
||||||||||||
2)
검정의 순서
◈
먼저 귀무가설 H0 을 세운다.「 차가 없다 」「 같은 모집단의
시료이다 」라는 형태이다.
H0
: μ1 = μ2 라는 가설을 세운다.
◈ 대립가설 을
정한다. 다음의 두 유형이 있다.
①
H1 : μ1 ≠ μ2
라는 가설을 세운다
('같지
않다' 즉 크거나 작을 수 있는 경우).
②
H1 : μ1 > μ2
( 혹은 μ1 < μ2 ) 라는 가설을 세운다
('~보다
크다' 혹은 '~보다 작다' 라는 경우)
①의
경우 [그림 1-19 ]와 같이 기각역이 분포의 양쪽에 있으며 양쪽검정이라 하고
②의
경우 [그림 1-20 ]의 어느 하나가 되어 기각역이 분포의 한쪽에 있는 한쪽검정이라
한다.
양쪽검정을
할 때는 분포의 양쪽의 기각역을 합하여 5 % 혹은 1 %가 되도록, 한쪽검정이면
한쪽만 5 % 혹은 1 %가 되도록 임계치를 확률표에서 찾는다 ( 표를 볼 때 주의가
필요한 사항 )
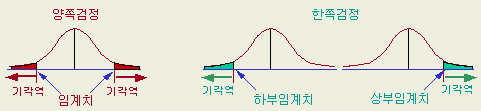
[그림
1-19 ]양쪽검정 [그림
1-20 ] 한쪽검정
◈ 유의수준을
정한다. 이 구역을 기각역이라하며, 유의수준은 5 % 와 1% 를 관행적으로 사용함으로
특별히 정할 필요는 없다.
◈
목적에 따른 적당한 통계량을 계산한다.
목적이라 함은, 검토의 내용이
평균치의 비교냐, 분산의 비교냐, 불량율의 비교냐에 따라 해당되는 분포가 각각
달라지게 된다. 정규검정, t 검정, F 검정, 카이제곱검정중 하나가 선택될 것이고,
시료에 대하여 구한 검정통계량을 z0, t0, F0,
Χ02 등으로 적는다.
◈ 확률표에서 유의수준에
따른 임계치를 찾고, 계산한 검정통계량 ( z0, t0,
F0, Χ02 등 )의 값과 비교한다.
z0, t0, F0, Χ02
등의 값이
① 유의수준
5 % 의 임계치 안쪽일 경우 (즉 기각역이 아니다) :「 유의하지 않다 」로 판정한다.
② 유의수준 5
% 이상 ~ 1% 미만일 경우 : 「 유의하다 」라고 판정한다.
③
유의수준이 1 % 이상일 경우 :「 고도로 유의하다 」라고
판정한다.
앞에서도 언급한 바 있지만, 두 군의 평균을 비교하는 검정에서도 분산의 동일여부에 따라 검정방법를 달리하므로 분산의 비교가 우선적으로 다루어야 된다.
두개의 시료 분산에 대해서 차가 있는가를 검정하는데는 다음 방법을 사용한다. 한개의 모집단으로부터 취한 두개의 시료에 대해서는 불편분산의 비가 F 분포를 함으로 측정치에서 구한 F0 의 값과 F 분포표의 임계치를 비교하여 F0 가 임계치보다 작으면 귀무가설을 채택하여 분산에 차는 없다고 판정한다.
검정의
순서는 다음과 같다.
◈ 귀무가설을 세운다.
H0
: σ12 = σ22
◈ 대립가설을
세운다.
H1
: 양쪽검정이면 σ12 ≠ σ22
한쪽검정이면
σ12 > σ22 또는 σ12
< σ22
◈ 각 시료에서 불편분산 V1,
V2를 구한다.
V1
= S1 / φ1 φ1 = n1
- 1
V2
= S2 / φ2 φ2 = n2
- 1
◈ 불편분산의 비 F0를 구한다. 단 F0가 1보다 커지도록
V1, V2 가운데서 큰 쪽을 분자로 한다.
예를 들어 V1> V2 이면 F0
= V1 / V2
◈ 유의수준을 α로 하면 F 표로부터
|
|
α = 5 % |
α = 1 % |
|
|
양쪽검정 |
0.025 표 |
0.005 표 |
기각역이 양쪽이므로 한 쪽은 그 1/2 에 해당. |
|
한쪽검정 |
0.05 표 |
0.01 표 |
|
◈
F0 ≥ F ( φ1 , φ2 : α/2 ) 이면
유의수준 α로 분산에 차가 있다고 판정한다.
F0
< F ( φ1 , φ2 : α/2 ) 이면 분산에 차가
있다고는 할 수없다.
|
{예제 3} 원료와 원료 에 의한 매일의 제품의 순도(단위: %)는 다음과 같다
원료 A와 B에서 순도의 날에 따른 산포에 차가 있다고 할 수 있는가? |
<
풀이 >
|
|
|
|
|
|
|
|
|
|
|
|
합계 |
|
xA |
74.9 |
73.9 |
74.7 |
74.3 |
75.8 |
74.2 |
74.4 |
73.3 |
75.5 |
74.0 |
745.0 |
|
xB |
75.2 |
75.0 |
75.3 |
76.9 |
75.0 |
74.9 |
74.4 |
76.5 |
75.3 |
|
678.5 |
|
xA2 |
5610.0 |
5461.2 |
5580.1 |
5520.5 |
5745.6 |
5505.6 |
5535.4 |
5372.9 |
5700.3 |
5476.0 |
55507.6 |
|
xB2 |
5655.0 |
5625.0 |
5670.1 |
5913.6 |
5625.0 |
5610.0 |
5535.4 |
5852.3 |
5670.1 |
|
51156.5 |
nA = 10 φA = nA - 1 = 9
nB = 9 φB = nB - 1 = 8
◈ H0 : σA2 = σB2
◈ H1 : σA2 ≠ σB2 (∵ 산포에 차가 있다라고 할 때, 클 수도 작을 수도 있는 양쪽검정이다 )
◈ 제곱의 합을 구한다.
SA
= ∑ xA2 - CTA = 55507.6 - (745.0)2
/ 10 = 5.08
SB
= ∑ xB2 - CTB = 51156.5 - (678.5)2
/ 9 = 5.09
◈
불편분산을 구한다.
VA
= SA / φA = 5.08 / 9 = 0.564
VB
= SB / φB = 5.09 / 8 = 0.637
◈
분산비를 구한다.
F0
= VB / VA = 0.637 / 0.564 = 1.13 (∵ VB
> VA 이므로 VB 를 분자에 )
◈
F표의 값과 비교한다.
F
(8, 9 : 0.025) = 4.10 > F0 (분자, 분모에 따른 자유도에 유의)
|
◇ 검정에서는 항상 유의수준 5 %값과 먼저 비교하여 유의한 경우 다시 1 %값과 비교하게 된다. ◇ 여기서 유의수준 5 % 값을 비교하는데 F (8, 9 : 0.05) 가 아니고, F (8, 9 : 0.025) 인 것을 이해하는가? 위의 [그림 1-7]과 같이, F분포표는 윗쪽의 확률만 표시하고 있다. 지금 이문제는 양쪽검정이므로, 양쪽 5 %를 보려면 한쪽은 그 1/2 인 2.5 % 즉 0.025 의 확률표를 찾아야 한다. |
◈
판정 : H0를 채택.
양쪽의 원료에서 순도의 날에 따른 산포에는
차가 있다고는 말할 수 없다 (「 산포에는 차가 없다 」라는 표현이 아님에 유의)
4-1)
σ 기지의 경우
시료의
평균값으로 부터, 이 시료가 정규분포를 하는 특정모집단 (모평균 μ, 모표준편차
σ) 으로 부터의 시료인가 아닌가를 검정한다.
|
σ 기지 (旣知) 와 σ 미지 (未知 ) |
|
◈
공정 (혹은 조건) 이라는 무한 모집단에서 σ
는 실제로는 알수 없는 값이지만 ◈ 그러나 보통 실험 데이터는 σ 를 모르고, 더욱이 샘플의 수도 작은 경우가 대부분이다. sample size n 가 30 개 이하일 경우를 소표본이라 하지만, 이 때에는 √ V 를 계산하여 σ 를 추정하여도 신뢰성은 매우 떨어진다. 그래서 이 때는 √ V 로서 σ를 대치하여 z 값을 구해서는 안되고, 정규분포대신 t 분포를 이용하여야 한다. ( 대소표본의 기준이 되는 sample size n = 30 개의 명확한 근거는 없겠지만, 30 개라면 정규분포로 취급할 때 약 4 %의 오차가 있을 뿐이다) |
검정의 순서
◈
귀무가설을 세운다.
H0
: μ = μ2
◈ 대립가설을 세운다.
H1
: 양쪽검정이면 μ ≠ μ2
한쪽검정이면
μ > μ2 또는 μ < μ2
◈ 시료평균
x 를 구한다.
x
= ∑ xi / n
◈ z0 를 구한다.
z0
= ( x
- μ ) / {σ / √
n}
◈ 정규분포표의 값과 비교한다.
z
(0.05 ) = 1.96 ≤ z0 이면 유의수준 5 % 로
z
(0.01 ) = 2.58 ≤ z0 이면 유의수준 1 % 로
로 유의차가
있다고 판정한다.
|
{예제
4}
어떤
공장에서의 약품의 수량(收量)이 종전 74.0 이었음을 알고 있다.
또 그 표준편차는 12.0 이었다. 새로운 장치로서 16회의 제조를
하였던바 수량의 표준편차는 변하지 않고 평균은 79.5 이라는 결과가
얻어졌다. 새로운 장치에 의한 종래의 수량이 변했다고 할 수 있는가 |
<
풀이 >
H0
: μ (기준) = μ0 (새 장치) H1
: μ ≠ μ0
z0
= ( 79.5 - 74.0 ) / (12.0 / √ 16
) = 1.89 < 1.96
유의차는 없다. 즉 수량이 변하였다고는 할 수 없다
◈
이 경우 '새로운 장치로 수량이 증가하였다고 (달라졌다고가 아니라) 할 수
있는가?' 라는 문제라면 즉 대립가설이 H1 : μ1 < μ2
로 되어야 하고, z 의 임계치로서 한쪽 5 % 값 ( 양쪽 10 % 에 해당 )
z
(0.10) = 1.64
와 비교하여야 한다.
|
대립가설에서 한쪽검정에의 유혹 (?) |
|
즉
통계량만으로는 다음의 두가지 판정이 가능한 위치이다.
이 때 초심자는 이 결과를 보고, 대립가설의 방향을 바꾸어 유의수준 5 %의 한쪽검정으로 대립가설을 채택하려는 유혹을 갖는다.(그렇게 한들 뭐가 잘못되는가? 처음부터 대립가설을 한쪽검정으로 세웠다고 하면 되지 않는가! 다르다고는 할 수 없는데 더 좋다라는 판정이 가능하다는 조화도 이상하고 등등 -- 옛날 저자가 경험한 갈등들이다) 앞에서도 언급했지만, 대립가설은 처음에 설정해야 하고, 한쪽검정은 어느 한쪽 (크다, 작다의 한쪽) 이라는 그 분명한 타당성이 인정될 때만 취급해야한다. 이 문제에서 새 장치가 나쁜쪽은 아니라는 분명한 타당성이 있을 때만이 한쪽검정을 할 수 있다는 것이다. 더 고급의 원재료를 사용하거나, 관리를 더 철저히 한다는 등등. 초등학교 4년생의 산수점수가 같은 문제의 3년생 점수보다 높을것이다고 한쪽검정을 해도 된다.
차가 '있다 없다' 라는 양쪽보다 '크다 작다' 라는 한쪽의 임계치가 더 severe해야 할 것 같은데 그렇지 않음은 왜 일까? 그것은 어느 한쪽은 분명히 아니라는 정보를 알고 있는 bonus이다. |
주2]
이 방법에는 새로운 장치로도 종래의 것과 산포가 변하지 않는다는 전제가 있다.
4-2)
σ 미지의 경우
(
실험등의 경우 모표준편차 σ 는 알려져 있지 않으므로 활용도가 높은 검정법)
σ
는 미지이므로 σ 의 추정치인 √
V 을 써서 t 분포를 이용한다.
◈ H0 : μ = μ0
◈
H1 : μ ≠ μ0 ( 양쪽검정 )
H1
: μ > μ0 ( 한쪽검정 )
μ < μ0 ( 한쪽검정 )
◈ x 와 √
V 를 구한다.
√
V = √ ( S / φ ) φ = n - 1 ( n
은 σ 의 추정에 사용한 데이터의 수)
◈ t0 의 값을 구한다.
t0
= ( x
- μ ) / { √
V / √ n }
◈ t 표의 값을 비교한다.
t
( φ, 0.05 ) ≤ t0 이면 유의수준 5 %로
t
( φ, 0.01 ) ≤ t0 이면 유의수준 1 %로
유의차가 있다고 판정한다.
|
{예제 5} 지금까지의 제조에서 금속제품의 강도의 평균 76.7 이었다. 새로운 용해로로 제조한 결과 다음표와 같은 데이터가 얻어졌다. 새로운 용해로로 강도가 증가했다고 할 수 있는가
|
<
풀이 >
수량의 표준편차의 추정은 표의 값에서 한다. 따라서 자유도는 9 (
= n - 1) 이다.
◈ H0
: μ = μ0
◈ H1 : μ < μ0
◈
제곱의 합 S를 구한다.
S
= ∑ x2 - CT = 62166.0 - 7882
/ 10 = 71.6
◈
√ V를 구한다.
√
V = √ ( S / φ ) = √
( 71.6 / 9 ) = 2.82
◈
시료평균 x
을 구한다.
x
= 788.0 / 10 = 78.8
◈
t0를 구한다.
t0
= ( 78.8 - 76.7 ) / ( 2.82 / √
10 ) = 2.36
◈
t 표의 값과 비교한다.「 강도가 증가하였다고 할 수 있는가 」라는 문제이므로
한쪽
확률 5 % ( 양쪽 10 %에 해당 ), 1 % ( 양쪽 2 %에 해당 ) 의 표의 값과 비교한다.
t
( 9, 0.10 ) = 1.833
t
( 9, 0.02 )= 2.821
t0
의 값은 이 사이에 있다.
◈
판정
유의수준
5 %로 강도는 증가하였다고 할 수 있다. 새로운 용해로로 바꾸어 좋은 제품이 나오게
되었다.
2조의 시료의 평균치의 유의차검정에는
t0
= ( x1 - x2 ) / { √
V × √ (1 / n1
+ 1 / n2 ) } (※)
를
사용한다.
단 √ V는 √ V = √ { S1 + S2 ) / ( φ1 + φ2 ) }
자유도는 φ1 + φ2 = n1 + n1 - 2 이다. 이 때 2조의 시료를 풀링해서 불편분산을 구하였으나 풀링할 수 있는 것은 2조의 시료의 분산에 유의차가 없음이 전제조건으로 되어있다.
즉 먼저 V1과 V2 에 대해서 F 검정을하여 F 가 유의아님을 확인하여 둘 필요가 있다. V1 과 V2 에 유의차가 있으면 위와 같이하여 √ V 을 구할 수 없으므로 따라서 윗 식을 사용할 수는 없다.
|
{예제 6} 원료 A와 원료 B에 의한 매일의 제품의 순도(단위: %)는 다음과 같다. 원료A 와 원료B 에서 순도의 평균치의 유의차를 검정한다.
|
< 풀이 >
|
|
|
|
|
|
|
|
|
|
|
|
합계 |
|
xA |
74.9 |
73.9 |
74.7 |
74.3 |
75.8 |
74.2 |
74.4 |
73.3 |
75.5 |
74.0 |
745.0 |
|
xB |
75.2 |
75.0 |
75.3 |
76.9 |
75.0 |
74.9 |
74.4 |
76.5 |
75.3 |
|
678.5 |
|
xA2 |
5610.0 |
5461.2 |
5580.1 |
5520.5 |
5745.6 |
5505.6 |
5535.4 |
5372.9 |
5700.3 |
5476.0 |
55507.6 |
|
xB2 |
5655.0 |
5625.0 |
5670.1 |
5913.6 |
5625.0 |
5610.0 |
5535.4 |
5852.3 |
5670.1 |
|
51156.5 |
이 데이터는 분산에 차가 없음을 { 예제 3 } 에서 확인하였으므로 평균치의 유의차 검정를 한다.
◈ H0 : μA = μB
◈ H1 : μA ≠ μB
◈
평균치 xA,
xB를
구한다.
xA
= 745 / 10 = 74.50
xB
= 678.5 /9 = 75.39
◈
양쪽의 시료를 풀링해서 불편분산을 구한다.
V
= (SA + SB ) / ( φA + φB ) = (
5.08 + 5.09 ) / ( 9 + 8 ) = 10.17 / 17 = 0.598
√
V = 0.773
◈
t0 를 구한다.
t0
= ( xA - xB ) / { √
V × √ ( 1 / nA
+ 1 / nB ) }
=
(74.50 - 75.39 ) / { 0.773 × √
( 1 / 10 + 1 / 9 ) } = -2.51
◈
t 표의 임계치와 비교한다.
t
(17, 0.05) = 2.110,
t
(17, 0.01) = 2.898
t0 는 이 사이에 있다.
◈
판정
유의수준 5 %로 평균치의 차는 유의이다. 원료 쪽이 싸며 또한 순도가
높음으로 원료를 구입하기로 한다.
|
{예제 7} 직물공장에서 직기의 사절수(絲切數)가 시간에 따라 차이가 있는가를 알아보기 위해서 다음과 같이 5 그룹으로 하여 직기 10대의 한시간당 사절수를 조사하였다. 시간에 따라 차이가 있다고 말할 수 있는가?
|
(풀이)
카이제곱분포의 설명을 참조.
사절수에 차가 없을 경우에 기대되는 값의 평균치는 9.6 이다. 따라서
X02 = { (13 - 9.6 )2 + (7 - 9.6 )2 + (13 - 9.6 )2 + (6 - 9.6 )2 + (9 - 9.6 )2 } /9.6
=4.50
X02
< X2 (4 ; 0.05) = 9.49 이므로 시간에 따라 사절수에 차가 있다고는
할 수 없다.
통계량으로부터 모수를 알아내는 일을 추정이라 한다. 추정치를 구하는 데는 다음의 두가지가 있다.
점추정
-- 어떤 한 점의 수치로서 모수를
표시한다. (33.0 mm, 65.3 kg 따위)
구간추정
-- 모수를 구간으로서 추정한다. (33.0 ±
1.6 mm 65.3 ±
2.7 kg 따위)
점추정은 분류상의 한 방법이기는 하지만 실제적으로는 표본의 평균일 뿐으로, 우리가 배우고자 하는 추정에서는 관심의 대상이 아니다.
모평균의
점추정은
x
→ μ
로 하고 모분산의 추정은
∑ ( xi - x
)2 / ( n - 1 ) → σ2
이다. 여기서는 구간추정에 대해
설명한다
2-1) σ 기지의 경우
샘플 평균 x 는 sample로서 취한 값
(x1, x2, …, xn )
의 함수로서 sampling
할 때마다 달라지므로 μ 에 완전히 일치한다고는 기대할 수 없다. 따라서 μ 를
하나의 값 x
로써
추정하기 보다는 예컨대 한
區間
( x
- k, x
+ k )
을 생각하여 이 구간 안에 μ 가 포함된다고 표현하고 싶다. 이런 구간추정에서는 95 %가 포함되는 범위를 사용하는 것이 일반적이다. (이 값을 신뢰도 혹은 신뢰한계라고 하며, 99 %는 참조용이라 할 수 있다)
우리는 앞의 1.2 정규분포에서 개개의 측정치 혹은 그들의 평균치가 모평균의 주위에 어떤 확률로 분포되고 있는지를 알았다. 모집단의 표준편차가 σ 일 때, 샘플 평균의 표준편차는 σ / √ n 이고, 표준화 측도 z 값에 따른 정규분포의 확률을 보이는 [표 1-1] 에서 95 %를 포함하는 z 의 임계치는 1.96 임을 알수 있다. 따라서 95 %를 포함하는 범위로서는 μ ± z σ 에서 z 값이 1.96 이다.
따라서 (개개의 xi 들은 μ ± 1.96 σ 이며,) 샘플의 평균치 x 로서는 μ ± 1.96 (σ / √ n) 가 된다.
거꾸로 x 를 기준으로 보면 x ± 1.96 (σ / √ n) 의 범위내에 μ 가 포함될 확률이 95 % 가 된다고 볼 수 있다.
일반적으로 확률 α 인 z 의 값을 z(α) 로 하면
x
- z(α)
( σ
/ √ n
) <
μ < x
+ z(α)
( σ
/ √ n
) (※)
下限
=
x
- z(α) ( σ
/ √ n
) 上限
=
x
+ z(α) (σ
/ √ n
)
의 범위가 모평균 μ 가 확률 (1 - α
) 로 있을 신뢰한계이고, 양쪽한계안에 있는 부분을 신뢰구간이라고
한다. 또한 추정에서의 확률은 항상 양쪽 확률을 이용하게된다.
◆ 구간의 폭을 결정하는 z(α) × ( σ / √ n ) 의 구성을 다시 한번 음미하시라. z(α), σ, √ n 이 무엇이며, 어디에 위치하여 값에 영향하는가를. 껄꺼러운 이런 식이 상식적인 사람의 수치에 대한 감각과 다를바 없음을 이해하시리라.
|
{예제 8} 어떤 제품의 수량이 종래의 공정에서 σ = 2.80 kg 임을 알고 있다. 이 공정으로 부터 랜덤하게 취한 크기 n = 16 의 random sample 의 평균치로 x = 15.70 kg 을 얻었다. 모평균의 95 % 신뢰구간은 얼마인가 ? |
< 풀이 >
95 % 신뢰도란 1 - α = 0.95 란 것이므로
∴
α = 0.05, z(α) = 1.96
따라서
下限
= 15.70 - 1.96 × 2.80 / √
16 = 15.70 - 1.37 = 14.33
上限
= 15.70 + 1.96 × 2.80 / √
16 = 15.70 + 1.37 = 17.07
∴ 신뢰도 95 %로 모평균은 14.33 ~
17.07 kg 의 구간에 있다 ( 아닐 확률이 5 % )
위의
구간은 어떤 특정한 sample에
의하여 계산한 것이다. 가령 다시 새로 뽑은 sample평균
( x
) 이
15.20 이 되었다고 하면 신뢰구간은
15.20
- 1.37 < μ < 15.20 + 1.37
13.83 < μ < 16.57
이라고 해석하게 된다.
이러한 신뢰구간이 모두 μ 를 포함한다고는 보장하지 못하므로, 어떤 특정한 신뢰구간 예컨대 (14.33 ~17.07) 이 μ 를 포함단다고 장담할 수는 없다. 다만 위와 같은 신뢰구간을 되풀이 해서 만들어 가면 그 중에서 95 %의 구간이 μ 를 포함한다고 말할 수 있을 뿐이다.
[그림 1-21 ] 은 μ = 15, σ = 2.80, n = 16일 경우에 sample을 20회 뽑아서 95 % 신뢰구간을 만들었음을 나타낸다.
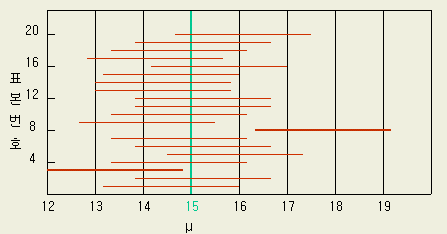
[그림 1-21] 20개의 신뢰구간
이 sampling 실험에 의하면 세번째와 여덟번째 sample 에서는 그 신뢰구간 안에 μ 를 포함하지 않는다. 그 원인은 전자에서는 샘플의 x 가 작게 나타났고, 후자에서는 x 가 지나치게 큰 값인 경우이다. sampling 을 여러번 계속하면 이와 같은 극단적인 sample 이 sampling 회수의 5 % 가량 나와서 추정이 들어 맞지않게 되나, 이렇게 판정할 때 95 % 는 올바른 추정을 하여 준다고 하는 것이 신뢰도 (신뢰계수) 의 의미이다.
◆
이 예에서 99 % 의 신뢰구간을 구하면 1 - α = 0.99,
∴
α = 0.01, z(α) = 2.58
이므로
下限
= 15.70 - 2.58 × 2.80 / √
16 = 13.89
上限
= 15.70 + 2.58 × 2.80 / √
16 = 17.51
즉 99 % 의 신뢰구간은 13.89 ~ 17.51 kg 이다 ( 신뢰도 95 % 에서는
14.33 ~ 17.07 kg 이었다)
이와 같이 신뢰도를 높이면 신뢰구간은 넓어진다.
( 추정에서
신뢰도를 높인다는 것이 '신뢰도' 란 단어가 의미하듯이 반드시 바람직하지는 않다.
즉 계수가 커지고 신뢰구간이 넓어져서 소극적인 추정이 되어 버리는 결과가 된다
( 신뢰도 99.9999 % 의 추정값이
무슨 의미가 있겠는가)
◆
또 n = 16 가 아니고, n = 4 의 경우, 95 % 신뢰구간은
下限
= 15.70 - 1.96 × 2.80 / √
4 = 12.96
上限
= 15.70 + 1.96 × 2.80 / √
4 = 18.44
로 되어 시료의 크기가 감소하면 신뢰구간은 넓어진다 ( 정도가
낮은 추정이 된다)
2-2)
필요한
sample의 크기
많은 sample일수록 추정이 정밀하게 되므로, sample을 충분히 크게 잡아서 목표로 하는 精度를 확보할 수 있다.
앞에서 μ 는 x ± z(α) × ( σ / √ n ) 사이에 있다고 추정하였다.
지금
신뢰계수를 100 ( 1 - α
) % 로 하였을 때 신뢰구간의 폭을 2 d 까지 허용한다면
( 치수의 허용차가 9.4 mm ~ 9.5 mm 라면 0.1 mm 를 2 d 로 보자는
의미이다. 즉 d = 0.05 mm 로 계산된다. 추정에서의 상하한의 구간의 폭이 2 d 이므로 )
d = z(α) × ( σ / √ n )
이다. 따라서 이 등식을 풀어서 필요한 sample의 크기 n을 정할 수 있다.
즉 n = { z(α) × ( σ / d ) }2 (※)
이 공식에 의하면 σ가 클수록 즉 모집단의 산포가 클수록 큰 sample 이 필요하다. 또 이 식을 이용할 때 의 σ 값을 정확하게 알아야 할 필요는 없고 과거데이터나 예비조사에 의해서 그 어림수를 알면 된다.
|
{예제 9} σ = 3 g 인 모집단에서 모평균 μ 를 허용오차 0.5 g 로 추정하려면 sample size는 얼마가 되어야 하는가? 단, 신뢰계수는 95 % 로 한다. |
< 풀이 >
d = 0.5, σ = 3, z( 0.05 ) = 1.96
n = ( 1.96 × 3 / 0.5 )2 = 138.3
이다. 즉 이 모집단에서 139 개의 샘플을 뽑아야 한다. ( 신뢰계수는 95 % 이므로 α = 5 % 의 위험율은 물론이다 )
|
sample size 에 대하여. |
|
측정의 정도를 향상시킨다 함은
d
= z(α) ×
( σ / √ n
)
그림에서 직관적으로도 이해되듯이 n = 1 로부터 n = 2 로 하면 √ 2 = 1,414 즉 약 30 % 좁아진다. 나아가서 n = 4 로 하면 √ 4 = 2.0 로 반으로 되나 더욱 반으로 줄이자면 √ 16 = 4.0 즉 측정회수를 12회나 증가시켜야 한다. 따라서 측정회수와 효율을 고려하면 5회 전후가 아닐까 ? |
2-3) σ 미지의 경우
σ
를 모르므로 σ 의 추정치인 √
V 를 사용하는 t 분포를 이용한다.
√
V = √ ( S / ( n - 1 )
를 사용하면
t0
= ( x -
μ ) / ( √ V / √
n )
인 통계량은 자유도 φ = n - 1의 t 분포를 함으로 이것을 사용하여 μ 를
추정할 수가 있다.
유의수준
α 의 t 의 값을 t (α) 로 하면 모평균 μ 의 신뢰도 1- α 의 신뢰구간은
x
- t
(φ, α) ( √
V
/ √ n
) <
μ < x
+ t
(φ, α) ( √
V
/ √ n
) (※)
이다.
복습
: σ 를 알고 (σ 기지) 정규분포를
이용한 다음의 식과 구성을 비교하라
x
- z(α)
( σ
/ √ n
) < μ <
x
+ z(α)
( σ
/ √ n
)
|
{예제
10}
비료를 25 kg 씩 포장하는 공정이 있다. 포대의 질이 바뀌었으므로
포장기의 조절을 하기에 앞서 10 개를 조사하였다. 평균은 얼마라
할 수 있는가? |
< 풀이 >
x
= 25.17
√
V 를 구하기 위하여
S
= ∑ x2 - ( ∑ x )2 / n
=
( 25.052 + 25.072 + … + 25.252 ) - (
25.05 + 25.07 +… + 25.25 )2 / 10
=6335.37-
( 251.70 )2 / 10 = 0.0836
√
V = √ { 0.0836 / (10 - 1)
}
=
0.0964
x ±
t (φ, α) × ( √ V / √ n
)
=
25.17 ± t (9, 0.05) × ( 0.0964 / √
10 )
=
25.17 ±
2.26 × ( 0.0964 / √
10 ) = 25.10 ~ 25.24
두개의
모평균의 차를 구하는데
x1
- x2 ±
t ( φ1+φ2 , α )×{ √
V × √
( 1 / n1 + 1 / n2 ) }
(※)
에
의한다.
|
분산의 가법성(加法性) |
|
치수가
다음과 같은 두 부품을 조립하는 경우 제품의 치수를 보자. ◆
가법성의 원리 |
( '분산의 加法性' 에 의하여 두값의 차의 합성 분산은 두 분산을 더하게 된다. 즉 평균치의 분산은 중심극한의 정리에서 V / n 이므로, 두개를 더하면 V1 / n1 + V2 / n2 이다. 두 분산은 같으므로 V × ( 1 / n1 + 1 / n2 ) 이다. 따라서 표준편차로서는 제곱근하여 { √ V × √ ( 1 / n1 + 1 / n2 ) } 이 된다 )
|
{예제 11} 원료 A 와 원료 B 에 의한 매일의 제품의 순도 (단위: %) 는 다음과 같다. 원료 A 와 원료 B 에서 순도의 차의 모평균의 신뢰한계를 구하라. 원료간에 분산의 차가 없음을 알고있다.
|
<
풀이 >
x1
- x2
= 0.89
t
( φA + φB , α ) = t (17, 0.05 ) = 2.110
양쪽의 시료를
풀링해서 불편분산을 구한다.
V
= ( SA + SB ) / ( φA + φB )
=
( 5.08 + 5.09 ) / ( 9 + 8 ) = 10.17 / 17 = 0.598
√
V = 0.773
따라서
0.89
± 2.110 × 0.773 × √
( 1 / 10 + 1 / 9 ) = 0.14 및 1.64
차의 모평균의 95% 신뢰한계는 0.14 ~ 1.64 % 이다.
|
{예제
12}
비료를 25 kg 씩 포장하는 공정이 있다. 포대의 질이 바뀌었으므로
포장기의 조절을 하기에 앞서 10 개를 조사하였다. 이 포장의 산포는
어떤 범위에 있는가 ? |
< 풀이 >
카이제곱
분포에서
{
S / X2 (φ ; α/2) } > σ2
> { S / X2 (φ
; 1-α/2) } (※)
의
구간에 모분산 σ2
가 있을 확률은 1- α 이다.
S
= ∑ x2 - ( ∑ x )2 / n
=
( 25.052 + 25.072 + … + 25.252 ) - (
25.05 + 25.07 +… + 25.25 )2 / 10
=
6335.37 - ( 251.70 )2 / 10 = 0.0836
신뢰도 95 % (α = 5%)로 하여
X2 분포표에서
X2
(φ ; α/2) = X2 (9 ; 0.025) = 19.02
X2
(φ ; 1-α/2) = X2 (9 ; 0.975) = 2.70
∴
( 0.0836 / 19.02 ) > σ2
> ( 0.0836 / 2.70 )
즉 신뢰도
95 %로 모분산 σ2
의 신뢰구간은 0.0044 ~ 0.0310 이다.
|
데이터에는 계량치와 계수치가 있다. |
|
계량치
(continuous data)는 길이나 무게 시간등 연속된 값을 취하며 측정하는
값이다. 5.0, 5.01, 5.001, … (g) 등으로
연속임을 알수 있다. 이들 값을 갖는 모집단은 정규분포를 갖는다. |