제1편 개론

         1장 품질공학이란

   
 

1.1   품질공학이란

1.2   왜 산포가 중요한가?                                           

1.3   Noise와 대책                                                       

1.4   SN比                                                           

1.5   直交表                                                            

1.6   왜 실험법은 품질공학인가?                           

이 장에서는 품질공학과 그 것에 사용되는 주요개념, 수법을 설명한다.   
 

 1.1  품질공학이란                                                    

 품질 공학에는 여러분야가 있지만, 그 핵심이자 根幹은 parameter설계인「타구찌법」으로「코스트를 올리지 않고 균일한 품질의 조건을 찾는 실험법」이다. 

종래의 실험계획법 (DOE : Design of Experiments)에서는 어떤 인자가 유의(有意)하며, 최적결과에서 제품이나 공정의 응답(실험결과인 특성치)이 어떤 값을 가질 것인가라는 인자의 함수로 모델화하는 것이다. 품질공학에 대비되는 특징의 하나는 실험에서 취급하지 않는 인자들을 일정한 상태로 유지시킴으로 실험에서 그 영향을 배제하려한다. 품질문제에서의 핵심적인 분산감소에 대해서는 무시한다.

이에 대하여 품질공학에서는 잡음인자 (제어할 수 없는 인자 즉 오차인자) 를 실험에 적극적으로 포함시켜 분산을 일으키게하고, 그러한 상황에서 잡음의 영향을 가장 덜받는 (강건한) 제어인자의 수준을 찾음으로써 산포가 작은  균일ㆍ 안정적인 제품의 조건을 찾는다.

품질 공학에서 '산포의 최소화' 라는 조건에서 '목표치에의 접근'을 다룬다. 즉 산포의 최소화가 우선한다고 할 수 있다. 만약 이 두가지가 서로 상치하게 된다면?  이 때는 손실함수를 이용하여 최적조건을 계량화할 수 있다.

현재 조업의 최적조건을 찾거나 특히 기술개발ㆍ상품개발의 초기 단계에서 이를 적용함으로 전체적인 개발 기간을 대폭 단축하고, 제품 생산이나 사용시의 트러블을 최소화할 수 있다.  

「 6 시그마 」활동의 개선단계에서 실질적인 도구로서 활용되고 있는「타구찌법」에는 제조공학의 핵폭탄으로 표현하기도 하는 구체적인 수법이 있다. 그 중요한 세가지 기술적 요소는 ① 손실함수 ② SN비 ③ 直交表 이다. 이 장에서는 이들 핵심요소를 설명함으로써 품질공학의 개략적인 이해를 돕고자 한다.

「품질공학」의 여러분야 중 因子 設計法(parameter design)을 한국과 일본에서는 「품질공학」, 미국등에서는「Taguchi Methods」「Robust Design」이라고 하는데 후자는 완건(頑健)설계, 강건(强健)설계로 번역하고 있다.
   이 홈페이지에서는 「품질공학」 「 타구찌법」을 구분없이 사용한다.

 

 

  1.2  왜 산포가 중요한가?                                           

 1) 품질의 정의 (품질 공학에서)

「품질이란 제품이 출하된 후 사회에 끼치는 손실이다.  단 기능 그 자체에 의한 손실은 제외한다」
   손실의 내용은
        ① 제품 기능의 산포에 의한 손실
        ② 폐해 항목(사용코스트도 포함)에 의한 손실
로 나눌수 있는데  ①은 산포에 의하여 기본적인 성능이 떨어지는 경우이며 ②는 약품의 부작용, 모터의 진동이나 소음, 수리비용등이 된다.   우리의 통상적 표현과는 거리가 먼 것 같지만, 품질을 정량화하기 위해서 적절한 정의라 할 수 있다.
   '기능 그 자체의 손실' 이란, 개인에 따라 TV 시청 그 자체를 싫어하는 사람도 있는 경우이다.

품질(quality)이란 제품의 유용성을 결정하는 성질 또는 제품이 그 사용목적을 수행하는 데 있어 갖추어야 할 성질 firnness for use 등으로 나타내어 왔다.

 

 2)  품질에 대한 사고방식

<그림1> 텔레비젼의 색상밀도의 분포

 

  <그림 1>은 「 SONY 텔레비젼 소비자 선호도 조사 」라는 아사히신문 (79 / 4 / 17) 의 게재 내용이다.  70년대 후반, 미국의 텔레비젼 사용자들은 SONY-USA보다는 SONY-JAPAN 제품을 더 선호하였다.  두 공장은 동일한 설계와 허용차로써 제품을 생산하고 있었는데, m은 목표 색상 밀도이며 허용한계는 m ± 5 이었다.  SONY-JAPAN의 제품 중 0.3%는 허용한계를 벗어나지만 SONY-USA는 벗어나는 것이 없었다.   따라서 규격한계를 기준으로 양 불량을 평가한다는 종래의 방식은 소비자의 선호도를 설명할 수 없게 되는 것이다. 

   3) 종전의 품질과 손실에 대한 사고

<그림2> 전통적 관점의 손실함수

 

 우리에게 낯익은 종전의 제품출하 검사에서의 사고와 손실은 <그림2>와 같이 규격한계를 정하여, 이를 벗어나기만 하면 벗어난 정도와 상관없이 일정한 손실 (A0 )이 발생한다고 보며, 마찬가지로 규격한계 안에 들기만 하면 손실은 없다고 보는 것이었다.

  규격한계치 전후에서는 약간의 특성치 차이로 손실이 0 혹은 A0 라는 불합리를 나타내게 되는 것이다.

 4) 손실함수 : 품질과 손실에 대한 Taguchi박사의 생각

 Taguchi박사는 아래의 <그림 3>에서 같이, 제품이 정확하게 목표치를 만족시키는 한 점 (m) 에서만 손실이 없고, 그 목표치를 중심으로 2차곡선으로 표현할 수 있음을 제시하였다. 여기에서는 합격불합격을 판정하는 규격한계가 품질손실과는 무관하다.

<그림 3> Taguchi의 손실함수

 

이를 수식으로 표현한 것이 다음의 손실함수이다.
      손실함수  L(y) = k ( y - m ) 2
여기서   k  : 품질손실계수
               y : 품질특성치
              m : 품질특성의 목표치
   식에서 품질손실은 목표치로부터의 벗어남의 제곱으로 영향을 미친다.

 5) 산포감소에 의한 손실효과

 ( y - m )2 을 분해하면  { ( y - y bar ) + ( y bar - m ) }2 가 되고, 제곱까지를 고려하면
( y - y bar ) 항은 분산 (variance), ( y bar - m ) 항은 목표치 m으로 부터 치우침(차이)의 제곱이다.

즉 품질손실은 ( 제품분산 + 목표치와의 차의 제곱 ) 바로 그것이다. 일반적으로 치우침의 수정 즉 평균치의 이동은 산포의 감소에 비하여  어렵지 않고,  만약 수정이 되었을 경우 손실함수는 분산에 비례한다. 따라서 산포에 따른 품질손실은 다음과 같다.

 

산포(표준편차)의 감소에 따른 품질개선 효과                           현재(기준)의 표준편차를 1로 볼 때

표준편차

1.0 (기준)

0.9

0.8

0.7

0.6

0.5

0.4

0.3

0.2

0.1

분산

1.0 (기준)

0.81

0.64

0.49

0.36

0.25

0.16

0.09

0.04

0.01

품질손실

1.0 (기준)

0.81

0.64

0.49

0.36

0.25

0.16

0.09

0.04

0.01

개선효과

0 % (기준)

19 %

36 %

51 %

64 %

75 %

84 %

91 %

96 %

99 %

표준편차가 현재의 70%로 줄어든다면 품질손실은 거의 반으로 되고, 품질안정에 의한 간접적 효과 (관리업무, 조업안정의 효과등)도 대단하다고 할 것이다. 종래에도 우리가 품질에서 산포의 중요성을 소홀히 한 바는 아니나, 이와 같이 금전적인 손실에 직결되며 더욱 그효과의 지대함을 새삼(?) 이해됨에 따라, 품질공학에서의 철학이라 할 散布 優先, 강건한(robust) 제조조건의 추구가 높이 존중받아야 할 이유이기도 하다.

 

 1.3  Noise와 대책                                                           

 품질 공학에서는 생산이나 사용에서 변동의 원인, 즉 제품이나 공정등 모든 시스템의 기능을 악화시키는 것을 noise라고 한다.  온습도, 먼지, 진동, 작업자의 습관ㆍ실수, 기계의 노후ㆍ마모, 원재료의 변동 등등이 그런 것이다. 기술개발이나 설계의 현장에서 목표 출력을 위한 도면의 설계나 조건설정은, 여러가지 noise를 줄이기 위한 싸움이 그 중심이라고 할 수 있다 (혹시 귀사에서의 주 戰場은 '중심치의  변화'이었다고 생각되시는가? 시운전상태에는 그럴 수 있지만) 

 1) noise의 분류와 대응책  

 종래의 기술개발에서는, noise가 없는 이상 상태로 만들려거나, 이상상태를 가정(온습도는 딱 맞게, 먼지는 없이, 원재료는 변동이 작은 것, 적당한(?) 숙련자가 작업한다는 등)해서 작업을 진행시켰다 .  진리 탐구를 목적으로 하는 자연과학에서는 적용될 수 있는 사고방식이나, 실제로 물건을 만들어야 하는 제조 현장에서는 非현실적이고 무엇보다 돈이 든다 (cost-up) 는 사실이다. 품질 공학은 noise의 개념과 그 취급을 적극적으로 하는 점이 특이하고, 기술개발에 실제적 기여를 하는 것이다.

  noise 대책에는, 이론적으로 다음의 세 가지 방법이 있을 수 있다. 
①  변동의 원인을 찾아내고, 원인 자체를 제거한다. (고급 원재료와 설비의 채택, 공조설비로 온습도 관리, 제품 사용조건의 제한등)
② 출력의 변동을 feed-back, feed-forward로 보정(補正)한다. (전후 공정의 온도 보정등 )
③ 변동의 원인에는 손을 대지 않고, 그 영향을 감쇠(減衰)시킨다. 

 지금까지의 전통적인 방법은 ① ②의 채택이었다.  그러나 ①과 ②는 무엇보다 비용이 들고 그 종류가 많아(재료나 부품, 기계, 작업조건, 관리등) 채택이 쉽지 않다는 것이다.   

 품질 공학에서는 ③의 방법을 기본적인 사고로 하여 noise에 영향을 덜받는(鈍感한), 즉 변동이 최소화되는 조건을 찾는다. 여기에는 일반적으로 cost-up이 따르지 않는다.   이렇게 하고도 품질이 목표에 미흡할 때에 ① ②의 방법을 보조적으로 채택하며, 이 때에는 경제성이 정량적으로 계산된다. 

 2 ) 품질공학에서의 대응책 예시

 품질공학에서 noise에 대한 접근방식의 개념이해를 위해 다음의 예를 보자. 
        (「實驗計劃法 제3판」 제17장  田口 玄一 箸 )


   일본의 伊奈製陶(1953년)에서는 타일의 휘어짐 뒤틀림등의 불량으로 합격률이 매우 낮아 고민을 하고 있었다.  원인은 가마 내부의 위치에 따라 소성(燒成)에서 받는 온도가 고르지 않아 타일의 변형율이 달라지는 것이었다. 

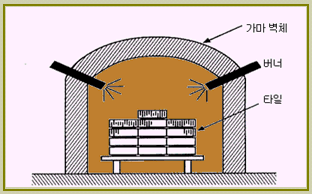
 전통적인 해결책은?
모든 위치에서의 온도가 균일하도록 설비를 개조하거나 전면적인 가마의 재설치라고 할 것이다. ( 실험을 한다면, 버너의 배치위치, 개수, 온도등 버너 중심의 실험이 될 것이다 ) 전면적인 재설치의 비용은 그 당시에 50 만$이나 되는 거액으로 채택하기 힘드는 수준이었다. 

품질공학에서의 해결책 - (총 27회의 실험에 사용된 인자와 수준은 다음과 같다)
◆ 점토(粘土)의 종류 (3종),       ◆ 납석(蠟石)의 양 (3종),       ○ 장석(長石)의 양 (3종),     
○ chamotte의 양 (3종),            ◆ 납석의 종류 (3종),             ○ 장석의 종류 (3종),     
◆ 어떤 첨가물의 양 (3종)

◆ 으로 표시한 것이  실험에서 有意한 인자로 확인된 것이다.  여기서 유의란, 이 들 인자의 수준을 바꿈에 따라, 위치에 따른 온도 차의 영향을 덜 받을(robust) 수 있다는 것으로, 이 들 인자의 최적구성으로 기존의 합격율 59%를 89%까지 향상시키는 획기적 성과를 얻었다. 

 이와 같이 품질공학에서는 noise의 근원을 없애거나 줄이는 방식이 아니라,  noise에 영향을 받지 않는 조건을 찾는다는 것이다. (위 실험에서 noise의 근원인 온도 혹은 버너에 대해서는 전혀 취급하지 않았음에 다시 한번 주목하자)

 품질공학에서는 noise의 영향을 받는 정도에 따라 「기능의 안정성」이 좋다, 좋지 않다 라고 하며, 그 척도로 SN比를 사용한다.

     

    1.4   SN比                                                           

  SN비는 본디 통신공학에서 사용된 것으로  (정보의 유효한 power) / (정보의 noise power )
 = (signal ) / ( noise) 라는 개념으로서 이 값이 클수록 선명하게 전달된다.
   
   품질공학에서 데이터에 대한 SN比의 식은
               η = 10 log ( m2 / σ2 ) = 10 log ( m / σ )2                                                                                  (※)
 여기서     η : dB(decibel) 단위의 SN比.      이-터(eta)로 읽음.
               m : 평균치
               σ : 표준편차

 식의 구성에서 σ가 작을수록 SN比는 커짐을 알 수 있다.  품질공학에서는 특성치의 종류에 따라 SN비를 구하는 식의 형태가 다르나,  식의 종류에 상관없이 어떤 경우에도 SN비는 클수록 안정성이 좋다.  대수값(log)을 취하는 이유는 산술적인 加法性이 향상되며, 10배를 하는 것은 사용하기 편리한 수준값으로 된다.

품질공학에서는 특성치 대신 SN比로서 데이터를 해석하여, 이로써 재현성이 높게 산포의 감소라는 至上 목적을 달성하려는 것이다.

 

   1.5  直交表                                                            

  직교표는 실험의 효율성과 精度를 높이는 위력적인 도구이다.  이것의 활용으로 실험의 양을 역 천문학적(?)으로 줄이며, 실험의 재현성을 높이고, 계산과 해석을 쉽게 할 수 있다. 또한 많은 인자를 넣는 실험이 가능하므로 효과가 높은 결과를 얻는다.
     여기서는 간단한「L9 직교표」로 원리만 설명한다. (직교표의 해설은 <제2편 3장 직교표> 참조)

註 : Taguchi 박사는 생애의 업적으로서, 직교표 활용에의 기여와 품질의 계량화라고 한 바 있다. 

 1) 실험인자와 수준

  특성치가 强度인 아래의 조건을 실험한다고 하자.

 

  온도, 원료, 촉매등을 인자(factor 혹은 parameter), 각 인자에서 실험하는 종류를 수준(level)이라 한다.  그러므로 이 실험은 각 3수준의 4인자 실험이며, 이 경우 정확한 해석을 위해서는 '3 의 4 제곱 = 81회'의 실험이 필요하다 (이유에 대해서는 다음 장에서)

 2) 직교표의 구성과 배치
   왼쪽이 직교표이고, 오른쪽이 앞에서의 인자와 수준을 실제로 배치한 것이다
 ① L9(34) 라고 직교표를 표기하며, 이것은 3수준짜리 4인자를 포함할 수 있으며 실험조건(실험회수)은 9개임을 의미한다. 보통 간단히 L9로 나타낸다
② 4개의 각列에는 실험할 인자를 배치한다.   제1열에 온도, 제2열에 원료, …, 등 4개까지 인자를 배치할 수 있다. no.1~ no.9 는 9종의 실험조건을 의미한다.
③ 내부의 1, 2, 3은 그 열에 배치한 인자의 수준을 표시한다. (색상으로 구분한 촉매열에서 수준배치를 이해하시라)

  실험no. 9 는 <온도 : 200 ℃ ← 3 , 원료 : 고급 ← 3, 촉매 : C2 ← 2, 시간 : 30분 ← 1>이라는 조건이며, 실험 결과 강도의 데이터는 18kg 을 나타내고 있다.  

 3) 인자효과의 계산

 직교표에서는 인자 (열)의 각 수준이 동일 회수 포함되어 있으며 (L9에서는 각 수준이 3회씩 포함) 평균치는 다음과 같다.

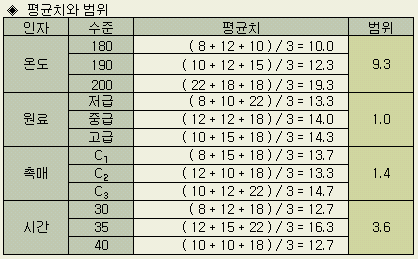
 각 인자에서 수준의 범위 ( = 최대치 - 최소치 )가 그 인자의 효과 (영향력)를 나타낸다고 볼 수 있다.  여기서는 온도 > 시간 > 촉매 > 원료가 그 순서라 할 수 있다. 해석의 다음 단계는 9.3  3.6 ....  1.0 등의 절대값이 의미가 있느냐는 것이다 (유의차의 검정)

여기서는 계산방법과 개념을 이해하기위해, 간단히 '범위'로 설명을 하나 실제로는 데이터의 분산(variance)을 이용하여 해석하는데 이것이 분산분석(ANOVA : Analysis Of Variance)이다. 

 4) 直交性 (직교표 사용의 이유)  

  9가지 조합실험에서 (온도, 원료)에 대한 1열과 2열의 조합 구성을 보자.  (1, 1) (1, 2) (1, 3) (2, 1) (2, 2) (2, 3) (3, 1) (3,2) (3, 3) 으로 된 것을 알 수 있다.  즉 온도 수준 1의 효과를 계산한 값 (8 + 12 + 10) 에는 원료의 수준1, 2, 3의 영향이 각 한번씩 들어 있으며, 온도 수준 2의 효과 (10 + 12 + 15), 온도 수준 3의 효과 (22 + 18 + 18)에도 마찬가지로 원료의 수준1, 2, 3의 영향이 한번씩 들어 있다. 즉 온도의 세가지 각 수준 계산에서 원료의 효과가 같은 양이 들어있다는 것은 원료의 영향은 배제된 오직 온도의 효과만이 포함된 데이터라고 볼 수 있다.   이것이 중요한 사실이다.   직교표는 어느 두열을 비교하더라도 이와 같은 구조로써, 다른인자의 간섭에 대해 걱정할 필요가 없다.  수학에서 직교(直交)라는 것은 서로 독립 즉 영향을 받지 않는다는 의미이다.

  종래의 실험에서는 어떤 인자를 실험할 때, 영향을 미칠 다른 인자는 수준을 고정시킴으로 그 영향을 배제하였다.  그런데 직교표에서는 다른 인자의  효과를 똑 같은(!) 양 포함시켜 그 영향을 배제하는 것이다. 두 방식 모두 논리적으로 타당하나 후자가 실험결과의 재현성 면에서 훨씬 유리하다. 

  5) 직교표의 효용 
     ①   많은 인자를 간단하게 배치하고 실험횟수가 적어도 된다 .  
 L9(34) 직교표의 9가지 실험은 조합실험일 경우  34 = 81회의 실험을 대체하며 품질공학에서 사용을 권장하는 18회 실험의 L18 직교표는 4374회 ( = 21 × 37 )의 조합실험을 대체한다.
    ②  종래의 개별인자 실험보다 훨씬 우수한 최적조건을 찾아낸다.
많은 인자를 포함시킬 수 있기 때문이며, 결과적으로 효과있는 인자의 선택가능성이 많아진다.    
    ③   실험결과의 재현성이 높다 (설명은 제2편 3장 직교표 참조).

 

  1.6  왜 실험법은 품질공학인가?                                  
  

품질공학의 효능을 증거하는 몇가지 사례


1)  Bell연구소는1980년 Taguchi박사를 초빙하여 미국 최초로 품질공학을 배웠다. 그 직후 Taguchi 박사의 직접 지도로, 그들의 숙원 과제였던 IC 칩의 수율개선에 착수하여, 종래 33% 수율을  87%까지  올리는 획기적 성과를 거둠으로 미국의 제조업계를 경악시키고, 품질공학이 미국에 알려지는 결정적 계기가 되었다.  ( Bell연구소는 AT&T와 Western Electrics 의 합자로 1925년 설립되어 11명의 노벨상 수상자를 배출하였고, 연구원 2만명의 세계 최대 연구소이다.  트랜지스터, Laser, 통신위성, 광통신, Cellular phone, Unix system과 C언어등 20세기 과학기술의 기념비적 발명들이 이 연구소의 소산이다)  

동 연구소의 Phadke 박사가 그들의 적용사례를 바탕으로 품질공학을 해설한 책(1989)은  국내에서도 번역되어 시판중이며, 서너권에 불과한 관계서적중에서 가장 추천하고 싶은 책으로, 그 첫머리에 게재된 내용을 이 글의 다음부분에 축약게재하였다.

2)   열처리제품의 경도(hardness) 산포는 표준편차로서 1 HRC 정도이고 0.3 HRC 라면 극히 좋은 수준으로 이해되고 있다. 또한 경도 標準片 (경도계의 보정기준이 되는 표준) 이라면 지금까지 0.2 ~ 0.3 HRC수준으로 알고 있다. 이것을 0.1 HRC 수준으로 하는데는 수십년이 걸릴 형편이다.   이 과제를 (株)旭工業所에서는 計量硏究所와 (財)일본베어링검사협회의 기술지도로 1년반만에 처음 목표로 한 0.1 HRC 이하를 달성하였다. 이것은 열처리 업계로서는 경이적이라 할 성과였다. 더욱 놀라운 사실은 이들 3者 모두 열처리에 대해서는 전문가가 아니라는 것이다. 12 내지 18 회의 실험을 몇차례한 종합레포트는 1991년도 ASI ( American Supplier Institute)의 제9차 Taguchi Method Sympisium에서 'Taguchi Award 최우수상' 을 수상하였다.
( 加工品質工學   矢野 宏 著  工業調査會 1994年刊에서 인용함 : 내용은 출판년도 기준 )

3)  일본의 top class 자동차부품회사인 DENSO에서는 매년 2,000건 이상의 타구찌법 실험을 하는 것으로 보고되었다. ( DENSO : 1949년 Toyota에서 분리독립한  '日本電裝' 의 새 이름)

 4) 강건설계를 이용한 품질공학         Phadke저  민영사
             (Bell연구소에서 수행한 실험내용을 토대로 만든 책이며,
             아래의 내용은 본문  p24~26 에서 그 들의 실적을 소개한 내용임)                                

     ① 부분 사진 植刻術(window photolithography)
                    공정의 분산 : 1/4로 감소
                    치명적 결함 : 1/3로 감소
                    공정처리시간 : 1/2로 감소
         ② 알루미늄 에칭(Aluminium etching)
                    가시적 결함 80%->15%
         ③ 탄탈륨 규화물의 반응이온 에칭에서 20일간의 실험으로
                    부식질(etching quality)의 불균질로 종래 웨이퍼의 18부분중 12부분만이 사용되던 것을                     17부분까지 쓸 수 있게 되었고, 기계이용률이 40% 증가.
         ④ 다결정 실리콘 증착(polysilicon deposition)
                    종래 단위면적당 10~5000개 정도의 표면결함을 10개이하로 유지.
         ⑤ 절단기 날 수명향상(Router bit-life improvement)
                    인쇄배선 기판을 자르는 절단기 날의 수명이 2~4배 개선.
         ⑥ 차동증폭기 회로최적화
                    회로인자의 새 명목치을 찾음으로 정격잔류전압을 40% 감소
         ⑦ 수용성 용제(water-soluble flux)를 만드는 원료의 최적구성비를 구함으로
                    波狀용접(wave soldering)공정과 용제성분의 인자를 찾음으로 결함률을 30~40% 감소
         ⑧ 컴퓨터의 UNIX 운영체계의 응답시간을 60%감소

 

   종래의 실험과 비교되는 타구찌법의 특장점
                ※ 진한 색상 표시의 항목은 일반 실험계획법(DOE)과도 차별화되는 특징이다.

        특         징

        설            명

① 품질의 균일ㆍ안정을 우선적으로 다룬다. 그러므로 균일한 조건을 구한다.

특성치가 아닌 SN비로 데이터를 해석한다.
 먼저 산포를 최소화하는 조건을 찾고, 다음에 목표치에 맞추는 2-step의 실험법이다.

② 대폭적인 품질개선을 이룬다

일반적인 실험에서는 인자를 많이 집어넣을 수 없지만 직교표를 이용하는 품질공학에서는 많은 인자를 넣을 수 있고, 유효한 인자들의 합계효과는 커질 수 있다 (Pareto도에서 중요한 몇개 인자의 합을 생각해 보라)

③ 적은 실험횟수로 소요기간이 짧다

일반적으로는 실험회수가 현장에서 감당할 만한 규모로 가능하다
(품질공학에서 권장하는 18회의 실험은, 종래 실험법에서 4374회의 조합실험에 상당하는 인자의 효과를 찾는다)

④ 비록 실험실의 실험 결과라도 현장에서 적용할 때 再現性이 높다.

직교표를 이용한 실험에서는 각 실험인자들이 잡음(오차의 원인)으로 작용되며, 그런 상황에서도 효과가 있다고 판정된 인자는, 다른 상황에서도 그 효과를 유지하게 된다.

⑤ 통상 cost-up없이 품질개선을 이룬다.

인자설계에서는 통상 cost-up없이 최적조건을 찾는다.

⑥ 확장성이 좋다.

 유사한 제품에서 실험결과를  적용할 때 또 다른 실험을 하지 않고 적용할 수 있는 확장성이 우수하다 (특히 동특성)

⑦ 품질의 계량화가 가능하다.

품질을 금액으로 계산할 수 있어, 의사결정에서 합리적 판단을 가능케 한다.

⑧ 직교표의 사용이 간단하다. 해석이 쉽다.

교호작용으로 직교표의 인자배치가 실험을 어렵게하고, 또한 채택하는 인자수가 줄어지는 일반적인 실험계획법에서의 문제가 없어진다.

       

  

◈ 품질공학 서적 ( 시판 도서)

    서      명

 저  자

출판사

(강건설계를 이용한) 품질공학  

Phadke (AT&T Bell)

민영사

(다구찌방법과 통계적 공정관리를 중심으로 한) 품질공학

박성현

민영사

 알기쉬운 다구찌기법

이상복

상조사

 다구찌 품질공학 해설

이우선

우용출판

     

◈ 도서관에서 구해 볼만한 책 (현재 절판)
  [품질공학강좌 ]  1991년 출판. 한국표준협회 -- 실험관련으로는 4권 1권 (3권) 의 순

 4권 [품질설계를 위한 실험계획법]

 1권 [개발설계단계의 품질공학]

 3권 [품질평가를 위한 SN비] 

 2권 [제조단계의 품질공학]

 5권 [품질공학 사례집 일본편 일반]

 6권 [품질공학 사례집 미국 유럽편]- 5권보다는 내용및 수준이 낮음

 7권 [품질공학 사례 계측편]