제1편 개론

       2장 종래실험의 과오

  

 

 

2.1   필요한 실험회수란 ?

2.2   단일인자 실험

2.3   종래 실험의 과오

2.4   실험계획법 - 「품질 공학」

종래 실험의 문제는 실험결과를 현장에서 적용할 때 잘 맞지 않는다는 즉 재현성 불량의 문제이며, 이런 경험들이 쌓여 실험을 통한 개발 ·개선이 더욱 소홀해진다는 것이다.  이 장에서는 왜 이런 문제가 발생하는지를 설명한다.

 

   2.1  필요한 실험회수란 ?                                       

 합성수지의 강도를 향상하기 위하여 아래와 같은 내용을 포함시켜 실험한다고 하자.

 앞章에서 설명한 바와 같이 온도, 반응시간, 촉매등을 인자(factor 혹은 parameter) 라 하고, 각 인자에서 실험하는 종류를 수준(level)이라고 한다.  여기서는 3인자 모두 3수준 실험의 경우로, 각 인자 모두 제2수준이 현행조건이라 한다.

인자간의 상호관계를 가지는 경우

  온도, 반응시간, 촉매등 모든 인자간에 서로 독립이라면(상관관계가 없는), 각 인자의 수준별로 실험을 하고, 좋은수준만을 합치면 최적조건이 된다. 이런 경우라면 실험법이랄 것도 없이 방법과 回數에서 간단하게 된다.
  그러나 온도와 반응시간은 고온에서 단시간이 좋으나, 저온에서 장시간 반응시켜야 하는 것이 일반적이다. 이처럼 다른 인자의 수준에 따라 어떤 인자의 효과가 달라짐을 인자간의 '交互作用 (interaction)' 이라고 하며,  교호작용이 있는 경우는 모든 조합으로 실험해보지 않고는 최적조건을 찾을 수 없다.
  공정에서 인자들 간의 교호작용의 有無는 전문가라도 쉽게 알 수 있는 것이 아니다. 그렇다고 모든 조합의 실험이란 더더욱 현실적이지 못함으로 실험의 신뢰성이 문제가 된다.

  실험에서 ' 많은 인자를 포함할수록 실험결과가 정확하다' 라는 공리(公理)가 있지만, 이것은 교호작용 때문이며, 이 실험의 경우, 인자의 모든 조합 형태(full factorial) 로 실험을 하자면 다음과 같은 조합의 구성이 된다.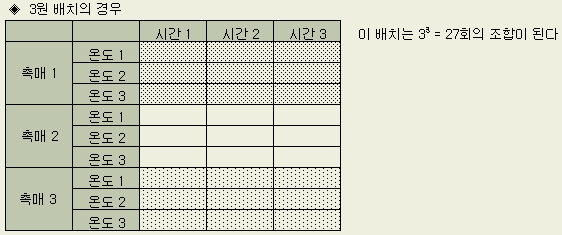

 이와 같이 수준과 인자에 따라 가능한 조합의 수는 아래와 같이 된다. 

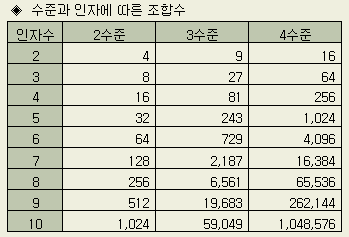
 단순한 공정이라고 해도 중요한 실험의 경우, 실험에 빠트리고 싶지 않은 인자수는, 표의 중앙부분에 해당될 것이며, 복잡한 공정이나 실험의 중요성으로 욕심이라도 부리면 표의 범위를 간단히 넘을 것이다 (제조조건 표준서에 기재된 인자의 종류를 생각해 보라). 표에서 보듯이 모든 조합의 수는 실제 실험이 불가능한 수치이므로, 현장에서 우리의 실험이란 아래와 같은 잘못된 길로 빠지는 것이다.

  

   2.2  단일인자(因子) 실험                                        

 현행의 공정조건이 각 인자의 제2수준이고, 강도의 평균이 8.5 (kg/㎟)이다. 

 1) 온도의 실험    먼저 온도의 조건을 바꾸어 다음의 결과를 얻었다.

 (온도를 제외한 모든 인자, 즉 시간 촉매만이 아니라 여기에 나타나지 않는 다른 인자의 조건을 가능한 고정시켜서 온도의 수준별 효과를 파악하는 것이다.)

 결론: 온도는 A3 즉 270도에서 좋다.

 2) 반응시간의 실험   시간에 따른 실험을 하여 다음의 결과를 얻었다. ( 앞에서 온도 A3가 최적으로 나왔다 하여 A3으로 하거나 혹은 종전 조건인 A2로 하나 의미는 같다.)

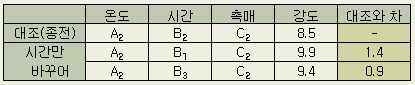
 결론: 시간은 B1 즉 60분이 좋다

 3) 촉매의 실험

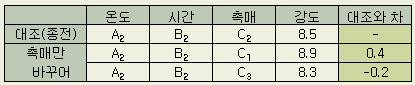
 결론: 촉매는 C1이 가장 좋다.

 4) 실험의 종합

 최적조건으로 온도 270도(A3), 반응시간 60분(B1) , 촉매 C1 이 선정되고, 종전 조건의 평균이 8.5 kg/㎟ 이므로 최적조건 (A3 B1 C1) 의 예상치로 8.5 + ( 2.0 + 1.4 + 0.4 ) = 12.3 kg/㎟ 을 기대하게 된다.

 그래서 확인실험으로 조건 A3 B1 C1으로 작업을 하였더니 종전 (8.5 kg/㎟) 수준에도 미치지 못하는 결과가 나왔다.

 왜 이와 같이 터무니없는 결과가 나오는가?    

만약 A1 B3 C1가 참된 최적 조건이라 가정해보자.

제대로의 실험이라면 논리적으로도 찾겨져야 하나, A의 실험을 할 때  B2 C2 라는 조건이므로 A1가 찾겨진다는 보장이 없다.( A의 실험때에 B3 C1 이라는 조건이었다면 찾겨질 것이다) 이하 다른 인자도 마찬가지. 참된 최적구성을 찾는 확율은 곱으로 되어, 여기서는 1/27 이다. 고로 27회의 '모든 조합'을 실험해야만 된다.

 

  2.3  종래 실험의 과오                                                

 1) 한정된 조건으로 부터의 결론을 아무렇게나 확장하는 잘못
온도 A3가 반응시간 B2에서 좋다는 결론일 경우, 반응시간이 B1, B3 에서도 A3가 좋다는 보편성이 없다.

 2) 조합의 영향 (交互작용) 을 생각치 않은 잘못
온도 A2에서는 시간 B1이 좋고, 온도 A1에서는 시간 B2가 좋을지도 모른다.  ( 반응온도와 반응시간의 경우 교호작용의 효과가 클 가능성이 많다 2) 두개의 인자의 조합에 의해 발생할 수 있는 교호작용을 고려하지 아니하는 잘못이다.

  3) 실험을 차례로 한 잘못(交絡의 문제)
실험순서의 random성이 확보되지 않을 때, 시간의 경과에 따른 영향 ( 숙련도 향상, 기온의 변동, 원부재료의 변경등 )이 섞여 확실한 결론을 내기가 어렵다.

 4) 실험오차와 산포를 감안하지 않는 잘못( 데이터의 통계적 처리 미비 )
실험오차와 변동의 해석을 못함으로써, 조건에 의한 차이인가 실험오차에 의한 것인가를 구별할 수 없어, ① 평균치만으로 ②주관적 판단을 하는 잘못을 범한다.

 5) 실험회수가 단 한번한 셈이 되는 실험精度의 불량.
종래의 방법에서 실험의 반복이 없다면 한번만 실험한 셈이다( 반복한다면 그만큼 실험회수가 증가하는 부담이 생긴다 ).  만약 어느 실험에 알지 못하는 실수가 있었다고 한다면 판단의 과오는 되돌릴수 없게 된다.

 

  2.4  실험계획법과 「품질 공학」                              

 위에서 설명한 과오들은 모든 조합을 실험하면 해결이 가능하나 엄청난 실험회수로 실제적일 수가 없다.  실험에서의 이런 불합리와 비효율에 대하여 19세기 말 영국의 농업시험에서 연구가 시작되었으며, 1920년대에 Ronald.A. Fisher에 의해서 실험계획법의 기초원리와 분산분석(Analysis of Variance)이 발표되고 그후 계속 연구되어 공업에 적용되기 시작하였다. 

 1947년 Rao에 의한 직교표(Orthogonal Array)의 적용은 실험의 효율화에 큰 기여를 하게되었다.  직교표에서는 많은 인자를 포함시킬 수 있으므로 개선의 기회를 획기적으로 높이고, 또한 실험결과의 재현성이 높다.

 이 홈페이지에서 다루는「품질 공학」은  일반적인 실험계획법(DOE : Design of Experiments)에서, 특히 품질의 균일성을 확보하는데 특장이 있는 최고의 실험법으로, 일본의 Taguchi Genichi박사의 연구로  1960년대 초 발표되었다. 이후 그를 주축으로 일본규격협회 중심의 연구와 보급이 이루어져, 70 ~ 80년대 이후 일본의 품질이 세계 최고수준을 확보하는데 품질관리와 아울러 큰 기여를 하였고, 1980년에 미국에 보급이 시작된 후 지금은 「6 시그마 」추진에서 핵심적인 실험법으로 자리하고 있다. 

 다른 실험법과 차이를 보이는 가장 큰 특징은 '코스트를 올리지 않고 균일한(변동이 작아 안정적인) 품질의 최적조건을 구하며, 품질을 定量化할 수 있다' 는 것이다.