직교표 (Tables of Orthogonal Arrays) 는 적은 실험회수와 해석의 간편성, 실험결과의 재현성,  많은 인자를 포함시킴으로 개선효과가 크다는 점등 본격적인 실험법에서 없어서는 안될 유효한 기법이다.

  3.1 직교표의 구조                                                   

◈   실험인자와 수준표
   

위와 같은 내용을 실험에서 다룬다고 할 때, 인자(factor)는 온도, 시간, …, 물의 5개이며, 각 인자 모두 2수준(level)의 실험이다. 직교표 실험에서 주로 사용되는 것은  2수준 혹은 3수준으로, 여기서는 모든 인자가 2수준의 실험이므로 아래와 같은 2 수준계의 직교표를 사용하게 된다.

아래 표의 왼쪽부분이 L₈ (2⁷) 직교표로, 2수준 인자 7개를 배치하여 8회 ( 8가지 조건) 로 실험한다는 표시법이다 (보통은 간단히 L₈로 표시한다). 제1행의 1 ~ 7을 列番이라 하며, 실험할 인자를 배치한다. 오른쪽 표에서 인자 배치의 실례를 보인다. 1열: 온도, 2열: 시간, ..., 5열: 물의 5개의 인자를 배치하고 나머지 두 개( 6열과 7열)는 비어 있다.

제일 왼쪽열의 실험no는 8종의 실험 조건을 나타낸다. 이 no.가 실제의 실험순서를 의미하지는 않는다.  일반 실험법에서 강조되는 실험순서의 랜덤화(randomization)를 직교표 실험에서는 심각하게 요구하지 않는다.

행과 열의 교차하는 곳에 1과 2는 각 열에 배치된 인자의 수준을 나타낸다. 구분이 쉽도록 2열과 3열에 수준별로 색상을 달리하였다. 위에서의 실험 수준표와 대비하여 배치의  의미를 이해하시라.

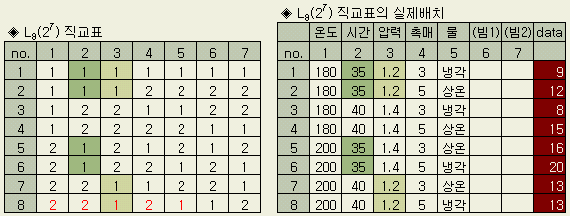
 따라서 실험번호 no. 8 의 실험조건은,  온도(2) : 200   시간(2) : 40    압력(1) : 1.2    촉매(2) : 5    물(1) : 냉각 이라는 배치이며 그 실험의 결과 측정값은 13 임을 나타내고 있다.

 6열과 7열은 인자가 배치되지 않은 빈열이며, 실험할 때는 전혀 고려할 필요가 없고, 실험 데이터를 해석할 때 오차로 계산한다.

 ◈   인자효과

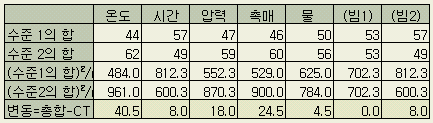
직교표에서 모든 인자(列)의 수준별 실험회수는 같다. L₈ (2⁷ )에서는 8회의 실험이므로 수준당 각 4회이다. '온도'의 수준별 합계는

              수준1 (180℃)의 합계 :  9 + 12 + 8 + 15 = 44 (실험no. 1, 2, 3, 4)
               수준2 (200℃)의 합계 : 16 + 20 + 13 + 13 = 62 (실험no. 5, 6, 7, 8)

마찬가지로 빈열을 포함한 나머지 각열을 계산한 것이 다음 표이다. (각 수준에 대해 4회의 반복실험이 되는 셈이다)

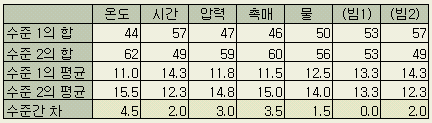
'수준간 차' 가 0 이라는 것은 무엇을 의미할까?  당연히  수준이 1 혹은 2로 달라지더라도 특성치에는 영향을 미치지 않는다는 뜻이다. 그러므로 표에서의 '수준간 차'가 특성치에 대한 영향력의 크기를 나타내며, 이 표에서 영향력의 순서는  온도 > 촉매 > 압력 > 시간 . 빔(2) > 물 > 빔(1) 이 된다.

  註: 모든 실험결과에 적용되는 내용이지만, 이런 효과는 실험에서 설정한 수준에서의 한정된 결론이고, 설정수준이 달랐다면 당연히 다른 결과가 나올 것이다. 실험결론을 확장하는 해석은 조심해야 할 것이다.

  3.2  직교성이란 ?                                                   

  위의 왼쪽 표는 보기 쉽도록 온도의 1, 2수준별로 색상을 달리한 것이다 (오른 쪽표는 6열 빔1을 기준으로 구분한 것)  여기서 온도수준1의 합계에 계산된 실험번호 #1, #2, #3, #4의 데이터란, 시간측으로 보면 (1수준 2회 + 2수준 2회)의 영향이 포함되어 있다. 온도수준2의 실험번호 #5, #6, #7, #8의 데이터에도 시간의 (1수준 2회 + 2수준 2회) 가 포함되어 있다. 즉 온도1, 2수준을 계산함에 시간의 효과가 같은 양 포함되므로 시간에 대해서는 영향받지 않는 온전한 온도만의 효과라고 볼 수 있다 (이것을 수학적으로 독립 혹은 직교라고 한다)

 이 온도의 데이터에 대해서는 압력 촉매등 다른 인자도 시간에서와 마찬가지로 동일한 양이 포함됨을 알 수 있고, 이런 성질은 직교표의 모든 열에 배치한 인자 상호간에 대해서 마찬가지다. 그러므로 직교표에서는 실험에 포함된 다른 인자에  영향받음이 없이 각 인자의 효과가 계산된다. 이 직교성에 의하여 적은 실험회수와 간단한 계산으로 인자의 효과를 구할 수 있게 된다.

  3.3 직교표의 종류                                                   

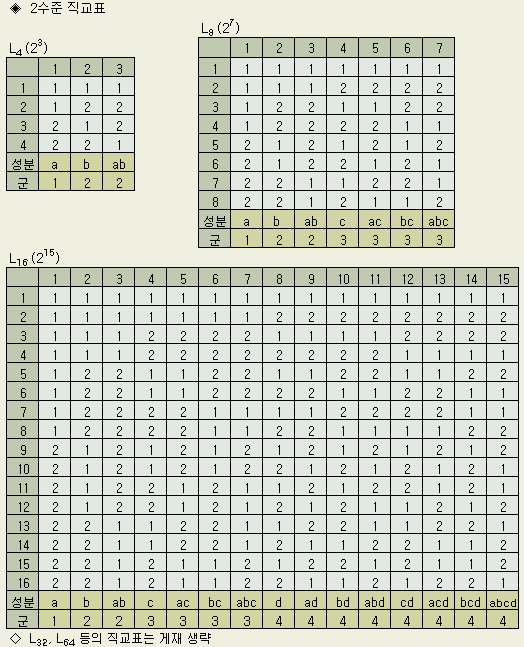
 1) 2수준 직교표

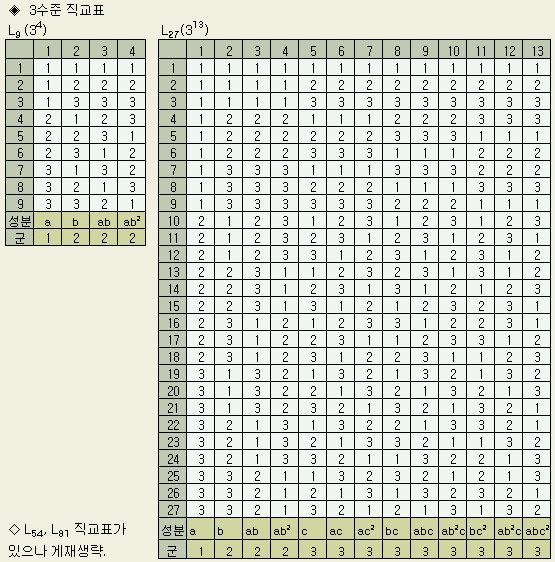
 2)  3수준 직교표

  3) 혼합계 직교표

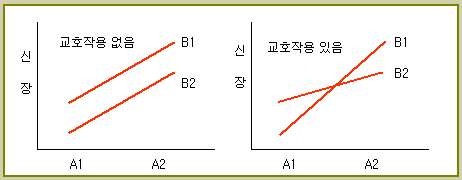
    어떤 2열의 교호작용 (아래 3.5 절에서 설명한다)은 특정열에 집중되지 않고 나머지 열에 조금씩 교락한다. 교호작용을 구할 수는 없다 ( 단   L₁₈ 직교표의 1열과 2열의 교호작용은 구할 수 있다 ). 품질공학에서는 혼합계 직교표의 사용을 권장하며, 실용적인 관점에서 L₁₈ 과 L₁₂이 많이 사용될 수 있다. 방대한 실험인 경우 L₃₆의 직교표를 사용할 수 있으나 실험회수가 현실적으로 부담스럽다.        

◈   L₁₈ 직교표에 대하여 (품질공학에서 사용을 권장하는 직교표)

  ①   2수준 1인자와 3수준 7인자 합계 8인자를 배치할 수 있는 직교표이다.  통상 현상 조건에서 상하로 어느쪽이 더 좋은지 분명치 않을 경우 3수준 직교표가 필요할 것이다. 3수준용 직교표라는 점과 현장에서의 실험회수라는 점에서 사용을 권장하는 직교표이다. (현장 실험이 필요하지 않는 simulation인 경우, L₃₆ (2¹¹*3¹²) 직교표는 많은 인자 (11+12 =23) 를 넣을 수 있는 직교표이다. 기업의 사활이 걸린 기술개발 혹은 개선실험은 36회 정도의 실험도 가능할 터)
   ②   2수준 인자 (제1열) 와 3수준의 첫째열 (제2열) 과의 교호작용은 구할 수 있다. 그러므로 2수준 인자와의 교호작용을 구하려는 3수준 인자는 제2열에 배치해야 한다. 그외 열은 교호작용의 배치를 고려할 필요가 없다.

◈    L₁₂ 직교표에 대하여

  ①    많은 인자를 채택해야 할 경우 2수준용이기는 하나  L₁₂ 직교표를 사용할 수 있다.
   ②   인자가 많을 경우, L₁₂ 직교표로 많은 인자 (최대 11개) 를 넣어, 어느 인자가 큰 영향을 미치는가 파악하고 (screening), 추려진 중요인자만으로 다시 L₁₈ 직교표 실험을 하는 것이 좋은 방법이다.

  3.4  분산분석                                                         

( 이절의 先修과정으로 [통계적 방법]에서「통계와 분포」「검추정」「분산분석」이 필요하다. 계산은 Excel로 자동화된다.)

 1) 변동 (제곱합)의 계산

      
여기서   n : 각 수준의 데이터 수 ( = 4)

수정항 CT는             
               CT = ( 데이터 총합 )² / 총 데이터 수
                       = ( 9 + 12 + … + 13 )² / 8 = 1405
A₁, A₂ 를 온도 각 수준의 합, n을 각 수준의 데이터 수라 할 때 온도(A)의 변동  S_A 는         
               S_A = ( A₁² / n + A₂² / n ) - CT = ( A₁² + A₂² ) / n - CT                                          (※)
                    = ( 44² + 62² ) / 4 - 1405 = 40.5

※   3수준일 때의 계산식은
                   S_A = ( A₁² / n + A₂² / n + A₃² / n ) - CT
                        = ( A₁² + A₂² + A₃² ) / n - CT                                                                      (※) 

 2) 분산분석표의 작성  
     
        
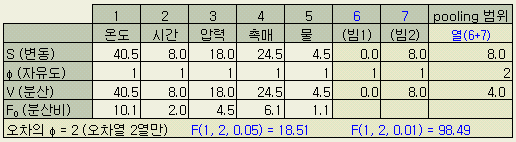
분산 V는      V = S / φ
φ : 자유도 (수준수 - 1). 모두 2수준의 경우이므로 각 열의 자유도는 1 이다.

여기서 오차로 배치된 열에 대해 생각해 보자. 앞에서 설명한 직교성을 생각해 보면, 오차열의 각 수준에는 다른 인자의 각 수준효과는 포함되지 않은, 샘플링오차와 측정오차 그리고 실험에서 다루지 않은 수다한 인자들의 영향들로서 실험의 精度라 할 수 있다. 그런 의미에서 오차 7열 (빔2) 의 분산 V가 8.0임을 생각하면, 분산 값이 이와 비슷한 시간(8.0)과 물(4.5)은 오차정도의 영향력을 갖는다 할 것이므로 오차에 합치는데 이것을 오차의 pooling이라고 한다. pooling에 의해 오차의 자유도가 커지면 유의차를 검정하는데 정밀도를 높이는 효과가 있다 (검출력의 향상)  위의 분산분석표의 제일 아랫줄의 F값 (2개열만 오차로 pool한 경우)과 아래 (4개열을 pool한 경우)의 F값의 한계치가 다름을 확인할 수 있다  (pooling에 의해 정도가 좋아질 수 있음을 본다) 

             pooling오차의 변동        S_(e) = 8.0 + 4.5 + 0.0 + 8.0 = 20.5
               pooling오차의 자유도     φ_(e) = 1 + 1 + 1 + 1 = 4
               V_(e) = S_(e) / φ_(e) = 5.1
_(e) 표시는 pooling한 값임을 나타낸다.

분산비 F₀ = V / V_e   단, V_e는 오차분산이며, pooling된 경우는 V_(e)를 사용한다.
  인자 온도의 F₀ = V / V_(e) = 40.5 / 5.1 = 7.9

만약 오차열이 없는 (모든 열에 인자나 교호작용이 배치된 ) 직교표의 경우, V값이 작은 2~3개의 인자를 pool하여 오차로 할 것이다.

 3) 분산분석표의 해석

      

  인자의 분산을 오차분산과 비교한 분산비 F₀가 작은 값이면 인자효과를 인정할 수 없고 ( 인자의 효과가 오차의 수준에 지나지 않는다 ), 큰 값이면 인자효과를 인정해야 한다는 것이 F분포를 이용한 검정방식이다. 그 판단의 기준값이 F(φ_A , φ_e , α)로서 φ_A : 인자의 자유도, φ_e : 오차의 자유도, α : 유의수준으로 5%와 1%값을 채용하며 통계서적의 부표로 나온다. ( 마지막 행의 유의수준 5%와 1% 값을 참조).

  각 인자의 분산비 F₀ = F(φ_A , φ_e , α) 가  F(1, 4, 0.01) = 21.20 보다 클 때 유의수준 1%로 (**표시) 유의라 하며, F(1, 4, 0.05) = 7.71 보다 클 때 유의수준 5%로 (*표시) 유의하다고 표현한다. 위 표에서는 온도만이 유의한 것으로 나왔다.

 검정의 논의이지만, 유의로 나타나지 않은 촉매 압력 (시간, 물까지도)의 실험결론은 "특성에 영향을 미치지 않는다"가 아니라 "이 정도의 실험으로는 (그 개수와 값) 영향을 미친다고 단정할 수 없다" 즉 판단의 보류인 것이다.

  3.5  교호작용과 열의 배치                                      

 1) 교호작용 列이란

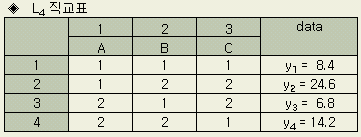
  이 표는 직교표에서 가장 간단한 2수준 3인자의 L₄(2³)  이다. 3.4 분산분석 에서 변동의 계산식을 다음과 같이 변환할 수 있다.
               S_A = ( A₁² + A₂² ) / n - CT
                     = ( A₁² + A₂² ) / n - ( A₁ + A₂ )² / 2n
                     = { 2A₁² + 2A₂² - ( A₁ + A₂ )² } / 2n = { A₁² + A₂² - 2A₁A₂ } / 2n
                     = ( A₁ - A₂ )² / 2n                                                                                          (※)
            ( 단, 2수준에서만 적용가능한 식이며,  n은 각 수준에서의 실험회수 즉 여기서는 n = 2 )

3열에 배치된 인자 C의 변동을 앞에서 변환된 식으로 나타내면
               S_C = ( C₁ - C₂ )² / 2n = { ( y₁ + y₄ ) - ( y₂ + y₃ ) }² / 4 로 된다

그런데 이 식의 ( y₁ + y₄ ) - ( y₂ + y₃ )은 ( y₁ - y₂ ) - ( y₃ - y₄ )로 나타낼 수 있다.
이것을 C이외의 인자조건에 착안하면 y₁은 A₁B₁, y₂ 는 A₁B₂,  y₃ 는 A₂B₁,  y₄는 A₂B₂ 이므로
               ( y ₁ - y₂ ) - ( y₃ - y₄ ) = ( A₁B₁ - A₁B₂ ) - ( A₂B₁ - A₂B₂ )가 된다. 이는
               A가 제1수준일 때의 B의 수준차 - A가 제2수준일 때의 B의 수준차
라고 할 수 있으며, 즉 A의 수준에 따른 B의 효과의 차이를 나타낸다. 이를 A와 B의 교호작용이라 한다. 즉 C의 변동으로 계산한 것이 실제로는 A와 B의 교효작용을 계산한 결과이기도 하다. 이와 같이 되는 것을 주효과 C와 교호작용 A × B가 교락(交絡)한다고 한다. 즉 C가 배치된 제3열에는 C의 효과와 교호작용 A × B가 섞여져 나타나므로 C의 주효과만을 알아낼수 없게된다. 

직교표에는 ① 2열간의 교호작용이 특정열에만 나타나는 것과  ② 여러 열에 분산되어 얹혀지는 것이 있다. 일반적으로 2ⁿ계 직교표( L₄, L₈, L₁₆등),   3ⁿ계 직교표( L₉ , L₂₇등)로 불리는 것이 ①의 경우 이며, 품질공학에서 권장하는 혼합계 직교표( L₁₂, L₁₈, L₃₆)는 ②에 해당한 다. ( 혼합계 직교표란 2, 3수준등 여러 가지 수준이 혼합되어 있다는 뜻이 아니라  교호작용이 어느 특정의 한열이 아닌 여러 열에 混在되어 나타난다는 의미이다 )

 2) 교호작용을 고려한 인자의 배치

앞절의 L₄(2³)직교표에서 제3열에 인자 C를 배치하면,  그 값에는 실은 A  B의 교호작용의 효과도 포함되게 되어 참된 C의 효과를 구할 수 없다는 것이다. A와 B의 인자간에 교호작용이 없다는 것이 분명할 때는 해당 열에 인자나 오차를 배치할 수 있다. 분명치 못할 때는 교호작용을 우선적으로 배치하고, 교호작용이 미치지 않는 다른 열에 인자를 배치해야 한다. 그러므로 인자배치를 빈열이라고 아무렇게나 배치할 수 없고 교호작용이 어느 열에 나타나는 지를 알아야 한다.( 현장의 고급 엔지니어도 인자간의 교호작용의 유무를 아는게 쉽지 않다. 이 골치아픈 문제는 품질공학에서 권장하는 혼합계 직교표를 사용하므로 해소할 수 있게 된다)

 교호작용이 나타나는 열을 아는 방법은
①   직교표의 성분표를 이용하는 방법
②   교호작용열표의 이용
③   線点圖의 이용
이다. 인자 배치의 實用的인 방법은 ③ ② ① 순이나, 설명의 차례는 그 반대가 되어야겠다.

 (1) 성분표에 의한 직교열의 확인

◈  2 ⁿ형 직교표

아래 L₈직교표의 제일 아래쪽 행에 쓰인 a, b, ab, …, abc를 각 열의 성분이라 한다. 교호작용이 나타나는 열을 알기 위해 열의 성분을 곱하되, 곱셈의 규칙은 제곱이 되면 1로 놓는다.
            즉 → a² = b² = c²≡1

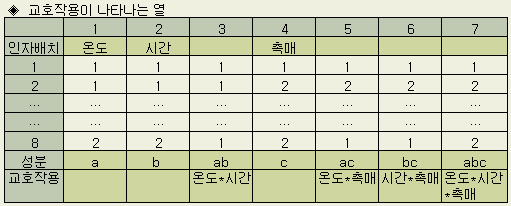
 1열과 2열의 교호작용은 그 성분을 곱한 ab 즉 3열에 나타나게 된다는 것이다. 마찬가지로 온도와 촉매의 교호작용은 ac 즉 5열에 나타난다. 1열과 5열의 교호작용은 a × ac = a²c→c 즉 4열에 나타난다. 6열과 7열의 교호작용은 bc × abc = ab²c²→a 즉 1열에 나타난다. 위표에서의 제7열은 3인자 교호작용열이나 일반적으로 3인자 교호작용은 나타날 가능성이 적으므로 고려하지 않아도 된다 (즉 어떤인자를 배치하여도 된다).

시간 × 촉매의 교호작용을 무시할 수 있다면 (기술적 경험에서) 6열에 인자를 배치할 수 있다 (이 배치에 따른 교호자용 열에 대해서 이미 배치한 인자와의 교락문제를 고려할 필요가 있기는 하다)

◈  3ⁿ형 직교표

 아래는 3수준 직교표인 L₂₇ (3¹³ )이다. 2수준 직교표의 설명과 함께 비교하여 참조하실 것.   

전체적으로는 2ⁿ형 직교표와 같으나 교호작용이 나타나는 열을 알기 위해                              
① 성분이 a, b 열이라면 ab열, ab² 열(또는 a²b열) 의 두열에 나타난다. (즉 두 성분 곱의 열과 한 성분 열의 제곱에 다른 열의 성분을 곱한 열)
② 세제곱이 되면 1로 변환.   → a³ = b³ = c³≡1
③ abc순으로 표기한 제일 앞문자의 指數가 제곱이면 전체를 제곱하여 정리한다.
                    a²b²c의 경우 → 제곱해서 a⁴b⁴c² →②항의 변환으로 abc²

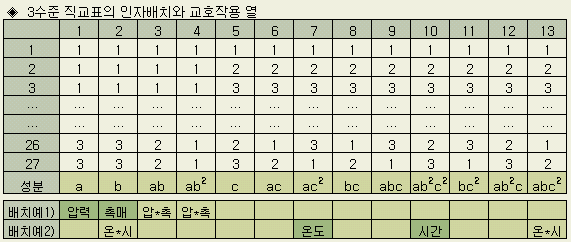
(예1)    1열(성분 a)과 2열(성분 b)의 교호작용은 어느 열에 나타나는가?
               a × b = ab  (3열),
               a² × b = a²b →a⁴b² → ab²   (4열)    
               a × b² = ab² (← a²대신 b²로 하여도 결과는 같다)
           즉 3열과 4열이다.  

(예2)    7열(ac²)과 10열(ab²c²)의 교호작용은 어느 열에 나타나는가?
               ac² × ab²c² = a²b²c⁴  →제일 앞문자가 제곱이므로 전체를 제곱해서
                   a⁴b⁴c⁸ → a³ab³bc³c³c² → abc²    (13열)               
               (ac²)² × ab²c² = a³b²c⁶ → b² →(b²)² → b⁴ →b   (2열)  

(2) 교호작용열 표의 이용 (배치때 보다 해석할 때 더 요긴하다)

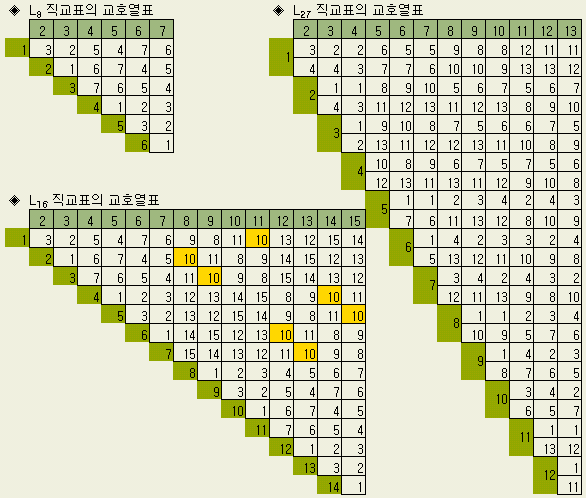
 ※ 교호작용열 표는 배치시에도 사용할 수 있지만, 해석할 때 더 요긴하게 사용할 수 있다. 즉 특정열의 값이 크다고 생각되거나, 특히 오차열이 큰 경우등은 교호작용이 교락되지 않았는가를 검토할 수 있게 해준다. 예로서 L₁₆ 직교표에서 제10열의 값이 이상할 때는 7개 (노랑바탕) 의 교호작용을 검토해 볼 수가 있다. ( 1열 × 11열, 2열 × 8열, 3열 × 9열, …  , 7열 × 13열 ).

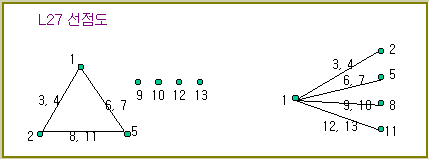
(3)  線点圖의 이용

① 선점도는 직교표의 각 열을 점과 선으로써 표시하여 교호작용이 어떤열에 나타나는 가를 바로 알수 있으며, 배치를 쉽게 한다.                                                                                       
   ② 숫자는 列番을 표시한다.                                                                                               
   ③ 점은 주효과, 선은 교호작용을 표시                                         
   ④ 실험내용에 맞게 어떤 선점도로 변형해도 좋다

◈   2수준계 직교표의 선점도 (L₁₆의 경우는 유사한 변형이 많다)

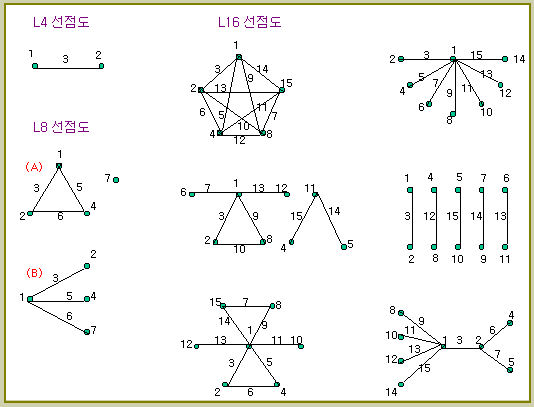
L₈ 선점도의 (A)
  1열과 2열의 교호작용의 열은 3열이 되고, 2열과 4열의 교호작용의 열은 6열이 되는 방식으로 점은 인자, 연결되는 선은 교호작용을 나타낸다. 떨어져 있는 7열은 다른 인자와 교호작용이 없는 인자를 배치할 수 있다.   

L₈ 선점도의 (B)
   하나의 인자가 다른인자와 교호작용이 많을 때 사용할 수 있는 경우를 나타낸다. 1열에 배치된 인자는2, 4, 6열에 배치된 인자와 교호작용을 나타낼 경우, 그 교호작용은 각 3, 5, 7열에 나타남을 의미한다.  
  선점도는 변형해 사용할 수도 있다.  위의 선점도 (A)에서 1열과 4열의 교호작용이 없다고 할 때는 그 사이의 선 5가 떨어져 나와 열7과 같은 단독 점이 되고, 인자를 하나 더 배치할 여유가 생긴다.       

◈   3수준계 선점도                                                                                                                                                                 

  3.6  직교표의 외측 할당 (배치)                                 

 SN비를 계산하기위해 신호인자나 오차인자를 표의 위쪽부분과 같이 직교표 혹은 일반 나열식으로 배치할 수 가 있다. 이를 외측 할당 또는 외측 배치라 한다. 이에 상대적인 표현으로, SN비를 비교하기 위하여 제어인자와 표시인자를 배치하는 main 직교표를 내측할당이라 한다. 위 표의 외측은 L₄ (2³)의 직교표로 배치된 경우이며, 외측할당은 실험회수와 직결됨으로 가급적 간단한 배치를 해야 할 것이다. 산포가 포함되는 SN비를 계산하는 경우, 외측할당은 최소 2조건 이상이라야 한다 (위 표에서는 4조건인 경우이다).

    3.7   직교표 사용의 특징                                                             

  ①   결과의 재현성이 높다  - 요인을 독립적으로 실험하는 것보다 조합하여 실험하는 편이 유리하다. 많은 인자를 동시에 취급하여 여러조건하에서 실험하면 다른 인자조건의 여하에도 불구하고 일관된 효과를 가지고 있는 것만이 분산분석에서 유의한 것으로 검정되어 신뢰성이 높다.
   ②   많은 인자를 간단하게 배치하고 실험횟수가 적어도 된다  

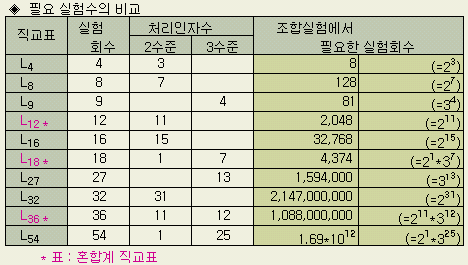
 조합실험 (Full factorial) 이란 모든 경우의 조합으로 실험하는 것이다.  품질공학에서 사용을 권장하는 L₁₈ 직교표의 경우, 필요한 조합 실험 4374회를 놀랍게도(!!) 18회로 대체할 수 있으며, 여기에서 구한 최적조건은 조합실험 4374회의 최적조건에 해당한다.   
    ③   보다 바람직한 최적조건의 결정  - 직교표 실험에서는 많은 요인을 취급하므로 선택될 수 있는 인자도 많아 보다 바람직한 최적해를 발견할 가능성이 크다. 요인을 하나씩 연구하는 경우는 상당한 진척이 있으면 더 이상의 연구를 중단해 버리는 경우가 많다. 직교표 실험에서는 최후까지 모든 데이터를 취하지 않으면 최적해를 구할 수 없으므로 실험을 서둘러 종합적 판단을 내리게 된다.
    ④   여러가지 인자의 조합조건으로 실험하므로 일반적으로 오차는 크다. - 그러나 실험의 결론에는 문제가 없다. 오차가 크더라도 그를 상쇄하는 통계적 해석을 하게 되기 때문이다.

◈   직교표에 의한 실험의 주의                           

①  교호작용의 존재여부에 대한 주의 (교락할 수 있는 가능성)  
  ②  실험이 복잡하므로 착오 유의    
  ③  결과가 기술적 해석과 상이할 경우 - 실험법, 해석법 및 고려에 넣지 못한 교호작용과 그 교락에 유의.