품질공학에서는 가능한 한 계량값을 취할 것을 권장하고 있지만, 그것이 불가능할 경우 등급분류의 데이터로 구해지는 경우가 있는데, 여기에는 계수분류, 계량분류, 다계량, 다계수값등이 있고, 주로 계수분류값의 해석법인 누적법, 정밀 누적법중 전자만을 설명한다 (정밀 누적법은 사례편과 관계서적을 참조하실 것).

  2.1  분류데이터의 의의                                            

  어떤 물품의 분쇄공정에서는 굵어도, 가늘어도 불량이며, 15 ~ 50 메시(mesh)의 것을 좋은 것으로 한다. 이 규격내가 100%로 되면 경제적이지만, 이 규격내의 %값으로 최적조건을 구하는 것은 적합치 않다. 현행조건이 A₁, B₁, C₁ 일 때 A₁ 을 A₂ 로, B₁ 을 B₂ 로, C₁ 을 C₂ 로 바꾸어 입도(粒度)의 수율을 조사한 결과 표와 같이 되었다.

  이 경우, A₁ 을 A₂ 로 하면 수율이 40% 증가하고, B₁ 을 B₂ 로 하면 50% 증가하며, C₁ 과 C₂ 간에는 수율에 변함이 없다는 사실을 뜻한다. 따라서 이 데이터로 보면 최적조건은 A₂ B₂ C₁ 또는 A₂ B₂ C₂ 이다.
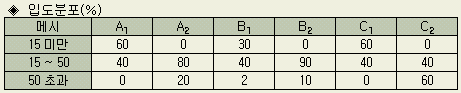
더욱이 이들 두 조건에서 수율은 100%에 가까울 것으로 예상한다. 그런데 실제로 A₂ B₂ C₂ 로 만든 결과, 수율이 10% 이하로 떨어진다면 담당자는 곤혹스러워질 것이다. 그러나 이 같은 경우가 발생할 가능성은 적지 않다.  왜냐하면 만약 15 메시보다 굵은 것, 50메시보다 가는 것의 분포가 다음 표와 같다면 현행조건에서 수율이 40%라는 것은 입자가 지나치게 크기 때문이다. C는 15~50 메시의 백분율은 달라지지 않지만, 입도분포에 가장 큰 영향을 미치고 있다. 따라서 위의 효과에서 알 수 있는 것은 C₂ 로 하기만 해도 입도가 가는 쪽으로 치우치기 때문에 A₂ B₂ C₂ 아래서는 수율이 상당히 낮아지게 된다.     

 이 경우 수율 데이터는 최적조건을 구하는 데 부적절하게 된다 . 만약 모든 조합에 대해 실험하면 최적조건을 알 수 있지만, 3수준 인자가 10개 있다면 조합의 수는 3¹⁰ = 59049개나 된다. 최적조건에 도달하는 실험을 하려면 특성값에 단조성(單調性)이 있어야 한다.  

 이 사례와 같이 입도가 어떤 범위안에 있을 때만 수율이 100%가 되는 문제에서는 수율의 데이터는 부적절하고, 지나치게 굵은 것과 가는 것의 양쪽 백분율의 데이터도 필요하게 된다. 이와 같이 3가지 백분율을 제시해 두면 A₂ B₂ C₂ 는 실험하지 않아도 최악의 조건임을 알 수 있다. 15~50 메시의 수율에는 단조성이 없지만, 3조의 백분율(계량 분류값이라 한다)에는 단조성이 있게 된다. 어떤 범위일 때에만 좋은 경우에, 수율을 백분율로 하거나 또는 상태를 좋다, 중간, 나쁘다라고 하는 경우에는 단조성이 없다. 可逆반응이나 과도한 반응에서의 수율, 균형(balance)이나 상태의 문제, 염색이나 페인트의 색조합, 기타 관능검사(상태, 맛, 냄새, 컨디션등)의 대상들이 단조성이 없는 경우이다.  선택한 특성치가 단조성이 있는지의 판단을 고유기술로 판단하는 일은 대부분의 경우 곤란하다 . 이런 경우에도 직교표에 따른 실험은 단조성의 평가가 가능하다.   

  2.2  등급분류의 데이터                                           

  1) 계수 분류값
   n회의 동작, n개의 물품이 몇 개의 조에 들어간 횟수와 개수로 주어지는 데이터를 계수 분류값이라고 한다.  계수 분류값은 일반적으로 다음과 같이 분류한다 .  

(1) 등급 설정의 데이터
   어떤 물품의 외관을 점수로 주면 계량값이지만, 상위 5개, 중위 20개, 하위 8개라는 형태로 분류하면 등급설정 데이터가 된다. 맛이나 분위기 등을 우, 량, 가, 불가로 분류한 것으로 사람에 의한 평가의 데이터에 많다.

  (2) 스케일 아웃의 데이터
   동물이나 물품의 수명시험에서 일부의 물품이 수명이 다되기 전에 실험을 중지했다고 하자. 예를 들면, 10개의 물품을 1000시간 수명 테스트했을 때 3개는 1000시간이 지나도 아직 사용할 수 있었다고 하자. 이 경우 수명을 다음의 5조
           Ⅰ: 처음부터 못쓰는 것
           Ⅱ: 1~100시간에서 수명이 다한 것
           Ⅲ: 101~500시간에서 수명이 다한 것
           Ⅳ: 501~1000시간에서 수명이 다한 것
           Ⅴ: 1001시간 이상에 수명이 다한 것
으로 분류하면, (1) 의 등급설정 데이터와 같이 취급할 수 있다. 일반적으로 스케일 아웃의 데이터에서는 일부 데이터는 계량값이지만, 일부는 어떤 값 이하 또는 어떤 값 이상이라는 데이터이다. 계량값의 범위를 3조 정도로 나누거나 수명과 같이 5조로 분류하면, 계수분류값으로 취급할 수 있다. 다만, 수명시험의 경우 시간의 인자 K를 K₁ = 0시간째, K₂ = 100시간째, K₃ = 200시간째, … K₁₁ = 1000시간째로 하여 각  K의 수준별로 10개의 물품이 살아있다면 1,  못쓰게 되었다면 0이라는 데이터로 하면 조수(組數) 2의 등급설정 데이터가 된다.

  (3) 게이지값
   정성분석에서 - (흔적 없음), + (흔적있음). ++ (흔적 많음)의 3조로 나눈 데이터처럼 본래는 계량값이지만, 그 크기에 따라 몇가지 조로 분류한 것을 말한다. Go-no-go gauge에서 통과하지 않은 것, 통과했지만 멈춤게이지를 통과하지 않은 것, 멈춤게이지도 통과한 것으로 분류한 것도 여기에 들어간다.
   플라스틱 제품이 몇도에서 ‘무르게’ 되는가 라는 취화(脆化) 온도를 구하는 경우 정확한 온도를 측정하기는 번거롭지만, 210 ℃에서 무르게 되었는지, 215 ℃에서 무르게 되었는지, 220 ℃에서 무르게 되었는지에 대한 테스트를 하면 게이지 값을 얻을 수 있다. 사람에 의한 관능검사의 데이터도 여기에 들어가는 경우가 많다 .

  (4) 순위의 데이터
 물품의 외관등 순위에 따라 배열할 수 있는 것을 말한다 . 같은 순위의 것이 여러 개 있어도 된다 . 그러나 몇 개 사의 물품의 외관을 비교하고자 할 때 자사(自社)의 것을 기준으로 잡아
           Ⅰ: 자사보다 나쁘다.
           Ⅱ: 자사보다 조금 나쁘다
           Ⅲ: 자사와 차이가 없다
           Ⅳ: 자사보다 조금 좋다
           Ⅴ: 자사보다 좋다          
의 5조로 나누어 (1) 의 등급설정 데이터로 하는 편이 좋다. 도형 같은 것은 여러가지 측면에서 순위설정을 하는 경우가 많다 .  

  (5) 순분류값
  몇가지 조로 분류된 데이터인데, 이들은 조에 대해 순위를 매길 수 없는 것을 말한다. 예를 들면, 불량의 종류와 형상으로 분류되는 경우의 데이터가 그런 것이다. 앞에서의 5종류의 계수분류값 가운데 (1) , (2), (3), (4)는 다음에 설명하듯이 누적법으로 해석할 수 있고 (5)는 도수법으로 해석할 수 있다.

 누적법으로 해석할 경우 데이터는 다음과 같이 다룰 필요가 있다 . 예를 들면, 데이터의 등급설정 분류가 우, 양, 가의 3조일 때 각각의 개수가 2개, 3개, 1개라고 하자.
     
  데이터 해석은Ⅰ조와 Ⅱ조만 하고 Ⅲ조는 해석하지 않게 된다. 즉 해석에 사용되는 조수는 (최초의 밀도도수의 조의 수 - 1) 이다.
  도수법의 경우에는 밀도도수의 상태로 하기 때문에 해석하는 조의 수는 밀도도수의 조의 수와 같다 .  

 2) 계량분류값
   계량분류값은 분류하는 각 조의 데이터가 계수분류값처럼 개수가 아니라 %(백분율)로 주어진 데이터이다. 예를 들어 설명한다.  

  (1)   입도 분포, 중합도 분포, 섬유길이 분포등 전체 개수가 불분명할 때의 분포
  어떤 입상물 (粒狀物)을
           Ⅰ: 25메시의 체를 통과하지 않는 것
           Ⅱ: 25메시는 통과하지만 50메시는 통과하지 않는 것
           Ⅲ: 50메시는 통과하지만 100메시는 통과하지 않는 것
           Ⅳ: 100메시를 통과하는 것
과 같이 4조로 나눈 데이터를 말한다.

 
   (2)   연속곡선의 데이터
  철판이나 필름의 두께, 온도와 점도 등과 같은 연속측정값이 있고 더욱이 그 값을 일정한 범위로 컨트롤하고자 할 때 다음과 같이 연속곡선의 값의 범위를 각 조로 나누어 각조에 들어간 비율로 한 데이터를 말한다.
     
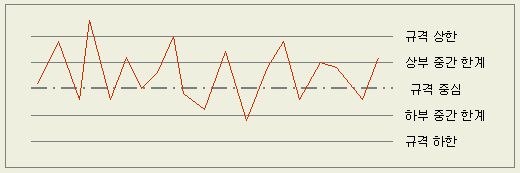
           Ⅰ: 규격상한을 초과한 경우 5%
           Ⅱ: 상부 중간한계와 규격상한 사이 15%
           Ⅲ: 상부 및 하부 중간한계 사이의 바람직한 값 80%
           Ⅳ: 하부 중간한계를 밑돈 비율 0%
           Ⅴ: 규격하한을 밑돈 비율 0%
와 같이 5조에 들어간 데이터를 구한다.
   만약 어느 구간을 100등분하고 이들의 각 점에서 곡선이 Ⅰ, Ⅱ, Ⅲ, Ⅳ, Ⅴ의 어떤 조에 들어가는지 데이터를 취한 경우에는 계수분류값의 게이지값으로 해석한다. 다만, 원래의 그래프가 있다면, 샘플링하여 몇가지 계량값으로써 망목특성의 SN비를 취해야 한다.

    (3)   순계량 분류값
  순위를 매길 수 없는 조에 대해 백분율이 부여된 것을 말한다 . 기술분야에서는 별로 사용하지 않는다. (1) , (2)는 누적법으로 해석하며, 이 때 해석하는 조의 수는 (최초의 수 - 1) 이된다. (3)은 도수법으로 해석하며, 이 때 해석하는 조의 수는 (최초의 조의 수)와 같다.

 3)  다계수값
  대, 중, 소의 흠집수, 큰 사고, 작은 사고의 수 등과 같이 몇가지 등급으로 나누어 각 등급별로 개수를 센 것을 말한다. 흠집의 숫자라도 대, 중, 소가 아니라 흠집의 종류별 개수를 분석하조자 할 때는 도수법으로 해석한다. 이 경우 누적법이든 도수법이든, 해석하는 조의 수는 (최초의 조의 수)와 마찬가지이다.

  4)  다계량값
   다이너마이트 파괴로 파낸 광석이나 암석을 그 입도분포에 따라 다음의 3조로 분류하여 중량을 측정했다고 하자.
            ① 지나치게 커서 재파괴가 필요한 것
             ② 적당한 크기로 파괴된 것
             ③ 지나치게 작아서 소결(燒結)이 필요하거나 운반이 곤란한 것
  합계 값이 불분명한 계량값을 몇가지 조로 분류한 데이터를 다계량값이라고 한다 . 이 경우 누적도수로 다음 3조의 중량
             Ⅰ : ①조의 중량
             Ⅱ : ①조와 ②조의 중량합계
             Ⅲ : ①, ②, ③조의 중량합계
를 해석한다 . 물론 해석방법은 누적법, 조의 수는 3조이다.

  2.3  분류 데이터와 SN비                                          

제품을 양 불량으로 분류하거나 정확히 동작하는지 여부 등, 상태를 2가지로 나누는 경우는 흔히 있다. n회의 동작중 정확하게 동작한 것을 1, 하지 않은 것을 0으로 하는 변수를 y₁, y₂, …, y_n 으로 한다. r 회 정확히 동작했을 때의 신뢰도 p는
             p = (y₁ + y₂ + … + y_n ) / n = r / n
로 주어진다.

전제곱합 S_T는
             S_T = y₁² + y₂² + … + y_n² = r          (f = n)
  평균값 p의 변동을 S_m으로 하면
             S_m = np² = n ( r / n )² = r² / n = ( np )² / n         (f = 1)
  따라서 오차변동 S_e는
             S_e = S_{T -} S_m = r - r² / n = np - ( np )² / n = np ( 1 - p )       (f = n - 1)
  참된 신뢰도를 p'로 하면 순변동 S_m'는 np' 이며  S_m의 기대값은 <1장.  변동의 해석>에서와 마찬가지로
             E(S_m) = S_m' + σ² = np'² + σ²
  한편, S_e 의 기대값은
             E(S_e) = ( n - 1 ) σ²
             ∴ E(V_e) = σ²
이다.

여기서 10 log (m² / σ² )에 상당하는 SN비를 생각해보면

                                                               

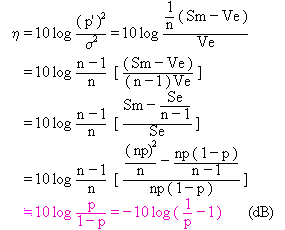
이를 오메가 변환이라고 하고, Excel의 log함수로 간단히 계산될 수 있다.

  2.4  계수분류값과 누적법                                       

  1) 누적법이란

특성값이 몇 개의 조로 분류되어 있을 때의 데이터로부터는 분포를 알수 있으며 분포를 만드는 것은 데이터의 산포를 보는 편리한 수단이다 . 품질개선은 산포를 작게 하는데서 시작되므로 분포를 비교하여 분포를 개선하는 것이 중요하다. 계량값의 경우에는 분포를 만들지 않고 산포와 평균을 종합적으로 파악하는 SN비를 개선함으로써 품질개선을 도모한다.
  누적법이나 정밀누적법은 원래 평균과 산포를 종합적으로 비교하기 위한 해석법이다 . 따라서 이런 해석법을 사용하는 것도 목적을 달성하는데 충분한 것이다. 간단한 사례로 설명한다.  

 2) 누적법에서의 변동

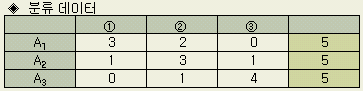
조립공정에서 사용하는 부품을 3종의 제조조건 A_1, A_2, A₃ 로 5개씩 만들고 결합상태를
             ① 너무 빡빡하다
             ② 적당하다
             ③ 헐겁다
로 분류한 데이터는 다음과 같다 . 이를 밀도 도수의 데이터라고 한다.  
    
   분포의 중심이나 분포형에 대한   A의 효과를 알아보고자 할 때의 해석법에 누적법이 있다. 앞에서 설명했듯이 ② 의 ‘적당하다’ 는 등급에만 주목해서는 안된다.
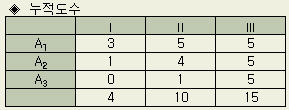
   분류의 조에 순서가 있는 경우에는 다음과 같이 누적도수를 만든다 . 순서가 있다는 것은 반드시 좋은순서 나쁜순서가 아니라 특성자체의 순서이다
           Ⅰ: ① 의 수
           Ⅱ: ① + ② 의 수
           Ⅲ: ① + ② + ③ 의 수
누적도수는 표와 같이 된다 .  

  
지금 Ⅰ조에 든 것을 1, 들지 않은 것을 0으로 하면 5개씩의 데이터는 표와 같이 표시할 수 있다.  

  
데이터가 0과 1밖에 없지만, 이것에 계량값과 같이 변동을 구하는 방법을 적용한다.

여기서 전변동 S_T (Ⅰ), A의 변동 S_A (Ⅰ), 오차변동 S_e (Ⅰ)는 다음과 같이 된다.  
             S_T (Ⅰ) = 1² + 1² + … + 0² - ( 1 + 1 + … + 0 )² / 15
                        = 4 - 4² / 15   (f = 14)
             S_A (Ⅰ) = ( A₁의 합계² + A₂의 합계² + A₃의 합계² ) / A_i 의 반복수 - (합계)² / 全 반복수
                        = ( 3² + 1² + 0² ) / 5 - 4² / 15    (f = 2)
             S_e (Ⅰ) = S_T (Ⅰ) - S_A (Ⅰ)    (f = 12)
다음에 Ⅱ조에 든 것을 1로 고치고, 들지 않은 것을 0으로 하면 다음 표가 만들어진다.  

  
 이 데이터에서 구할 수 있는 전변동을 S_T (Ⅱ), A의 변동 S_A (Ⅱ), 오차변동 S_e (Ⅱ)라 하면
             S_T (Ⅱ) = 10 - 10² / 15   (f = 14)
             S_A (Ⅱ) = ( 5² + 4² + 1² ) / 5 - 10² / 15    (f = 2)
             S_e (Ⅱ) = S_T (Ⅱ) - S_A (Ⅱ)    (f = 12)
 Ⅲ조는 반복수가 되므로 해석 대상에서 제외된다 .

이들 2개의 조에서 별도로 구해진 변동을 합쳐 하나로 정리하면 된다. 여기서 Ⅰ조의 전변동 S_T (Ⅰ)를 다음과 같이 고친다.
              S_T (Ⅰ) = 4 - 4² / 15 = ( 4 × 15 - 4² ) / 15
                         = 15 × 4 / 15 × ( 1 - 4 / 15 )
                         = 15 × PⅠ × (1 - PⅠ ) = 2.93
    단,  PⅠ는 Ⅰ조에 든 비율 4 / 15 이다,
  마찬가지로
               S_T (Ⅱ) = 15 × 10 / 15 × ( 1 - 10 / 15 )
                          = 15 × PⅡ × (1 - PⅡ ) = 3.33
    단,  PⅡ : Ⅱ조에 든 비율
이 된다 .

 이는 전변동 S_T 가 각조에 들어가는 비율 P에 의해 데이터 수 n의 P(1 - P)배가 된다는 사실을 나타낸다. 즉, 조의 비율 P가 0.5일 때 변동은 최대가 되며 P가 0 또는 1에 접근함에 따라 작은 값이 된다. 전변동이 그런 상황이므로 다른 요인효과도 P의 크기에 따라 그 상대적인 크기로 평가된다. P가 서로 다른 조의 변동을 같은 비중으로 합하는 것은 좋지 않다. 적당한 척도가 필요하게 된다.

 조의 비율이 P일 때 전변동이 P(1 - P)배로 평가되는 것이므로 그 역수인 1 / P(1 - P)를 각조의 변동을 종합할 때의 가중치로 하려는 것이다.

 즉 Ⅰ조의 변동에는
              W₁ = 1 / { PⅠ ( 1 - PⅠ) }
                    = 1 / { ( 4 / 15 ) × ( 1 - 4 / 15 ) }
                    = 15² / { 4 × ( 15 - 4 ) }
                    = n² / { r × ( n - r ) }                                                                                        (※) 
                    = 5.11
  Ⅱ조의 변동에는
              W₂ = 1 / { PⅡ ( 1 - PⅡ) }
                    = 1 / { ( 10 / 15 ) × ( 1 - 10 / 15 ) }
                    = 15² / { 10 × ( 15 - 10 ) }
                    = 4.50
을 곱하여 종합한다 .

 지금 종합한 전변동을 S_T, A의 변동을 S_A 오차변동을 S_e 으로 하면
              S_T = S_T (Ⅰ) W₁ + S_T (Ⅱ) W₂                                                                                    (※)
                   = 15 × 4 / 15 ( 1 - 4 / 15 ) W₁ + 15 × 10 / 15 ( 1 - 10 / 15 ) W₂
                    = 15 + 15 = 30    (f = 14 × 2 = 28)
  일반평균을 뺀 전변동은
              S_T = 측정수 × ( 분류의 조 - 1 )
로 표시된다.
              S_A = S_A (Ⅰ) W₁ + S_A (Ⅱ) W₂                                                                                    (※)
                   = { ( 3² + 1² + 0² ) W₁ + ( 5² + 4² + 1² ) W₂ } / 5 - CT
                   = 48.02 - 35.45 = 12.57   (f = 2 × 2 = 4)
         단, CT = ( 4² × W₁ + 10² × W₂ ) / 15 = 35.45
              S_e = S_T - S_A = 30 - 12.57 = 17.43    (f = 24)

분산분석표는 다음과 같다 .
     
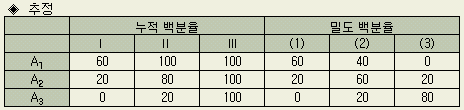
  A의 효과는 부정할 수 없으므로 어떤 수준이 좋은지를 결정하게 되는데, 이 사례에서는 인자가 A뿐이므로 수준별로 백분율을 구하고 분포상황을 그래프로 만들어 판단한다.

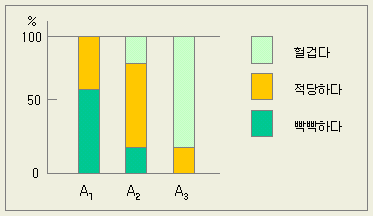
 분류한 조의 순서에 따라 ‘좋다’ ‘나쁘다’가 결정되는 경우의 최적조건은 ‘좋다’는 비율이 많은 수준을 선택하는데, 이같이 제(2)조가 가장 좋은 경우는 간단하지 않다. 이 경우 (2)가 많은 것은 A₂ 이지만 빡빡하다, 헐겁다는 것은 지름의 대소로 결정되는 것이므로 조정인자로 지름의 평균값을 바꿀 수 있을 지도 모른다. 만약 그것이 가능하다면 A₂ 보다는 A₃ 쪽이 좋다고 할 수 있다. A₃는 이대로는 ‘헐겁다’는 비율이 80%를 차지하는데. 평균값을 바꾸면 ‘적당하다’는 비율이 늘어나게 된다. 그러나 이런 판단은 정량적이 아니다. 어디까지나 하나의 방향을 제시해 주는데 불과하다. 이 같은 면에서도 가능한 한 계량값을 취하여 SN비에 의한 해석을 하도록 권장하는 것이다. 그러나 실제로 제조현장에서 사용하는 경우가 많으며 사례편의 예로써 풀이를 이해하시기 바란다.