|
제3편 상론 (고급) 3장 직교표의 變用 |
|
3.1 더미(擬水準) 법 3.2 조합법 3.3 다수준 작성법 3.4 의인자법(변신법) |
直交表
실험에서 상황에 따라,
「3 수준의 열에 2 수준을 배치하고 싶다」 「L18
직교표에서 6 수준 인자를 배치하고 싶다」는 등, 直交表를 그대로 사용하는 것이
아니라 일부 변경해야 할 필요가 생긴다. 이와
같은 直交表의
응용 배치법중에서 더미법,
조합법, 다수준 작성법, 의인자법에 대해 설명한다.
3 수준의 열에 2 수준을 배치하는 방법으로써 dummy법이 있다.
dummy란, 2수준의 인자를 형식적으로 3수준으로 하는 방법으로, 2수준 중에서 중요하다고
생각되는 것을 중복시켜 배치한다.
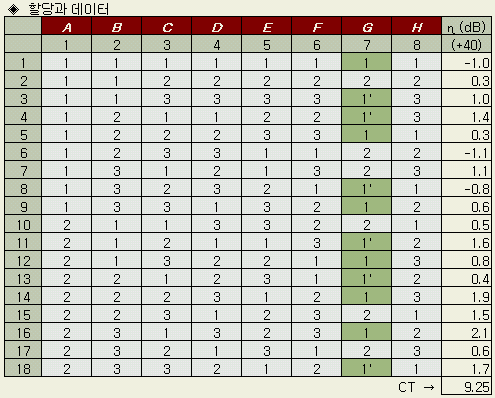
L18 直交表에서 2수준의 인자가 A, G 2개 있을 경우 A를 제1열에 배치하고, G는 제7열에 배치한다고 하자.(아래 예제의 직교표 배치를 참조) G1, G2 중 더 의미가 있을 것 같은 G1을 G3에 배치한다면 G1 = G1 G2 = G2 G3 = G1' 로 된다.
◈ 변동의
계산
SA
= ( A12
+ A22
) / 9 - CT (f = 1)
SB
= ( B12
+ B22
+ B32
) / 6 - CT (f = 2)
C, D, E, F, H의 경우는 B와 같으나,
G는 다음과 같다.
SG
= { ( G1
+ G1’
)2
/ 12 + G22
/ 6 } - CT (f = 1)
(※)
G1
과 G1’
은 본래 같은 수준이므로 차이가 없을 것이다. 여기서 발생한 차이는 오차의 일부이다.
이를 더미간의 오차라 하며 다음식으로 구할 수 있다.
Se
= { ( G12
+ G1’2
) / 6 } - ( G1
+ G1’
)2
/ 12
= ( G1
- G1’
)2
/ 12 (f
= 1)
< Dummy법의 실험예 >
디젤엔진의
NOx
대책으로 2수준의 A, G인자와 3수준의 B, C, D, E, F, H인자를 직교표 L18
에 할당하고 외측할당으로 오차인자 3종의 운전조건 아래 NOx를
ppm 단위로 조사했다. NOx
는 적을수록 좋으므로 망소특성으로 SN비를 구했다. 할당과 데시벨 단위의 SN비는
다음표와 같다. 단, G는 7열에 dummy법을 적용하기 위해
G1
= G1
G2
= G2
G3
= G1’
로
했다.
현행조건은 A1
B2
C2
D2
E2
F2
G2
H2
이다.

보조표를 작성하고 변동을 계산한다. 데이터는 가평균(40)을 뺀 것이다.

CT
= 12.92
/ 18 = 9.25
ST
= - 1.02
+ 0.32
+ 1.02
+ …
+ 1.72
- CT
= 15.445
(f
= 17)
SA
= ( 1.82
+ 11.12
) / 9 - CT = 4.805
(f
= 1)
SB
= ( 3.22
+ 4.42
+ 5.32
) / 6 - CT = 0.37
(f
= 2)
이하 C, D, E, F, H는 SB와
계산식이 같다.
SC
= 0.040
(f
= 2)
SD
= 0.123
(f
= 2)
SE
= 0.303
(f
= 2)
SF
= 7.410
(f
= 2)
SH
= 1.803
(f
= 2)
SG
= { ( 4.7 + 5.3 )2
/ 12 + 2.92
/ 6 } - CT = 0.49
(f
= 1)
Se
= ST
- ( SA
+ SB
+ … + SH
) = 0.101
(f
= 3)
註
:
L18
계산에서 2수준이 제1열과 더미 처리열이므로 이 열들의 변동 계산식과 자유도 f
에 대해서 주의할 일. 직교표에서 인자별 자유도는 (수준수 - 1) 이다.
註 : Se의
자유도 3은 1열과 2열의 교호작용인 2와 더미열에서 빠져나온 1을 합한 값이다.
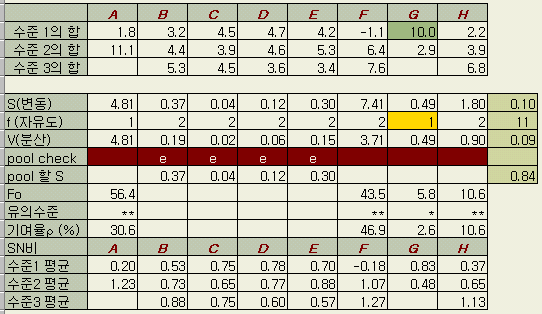
이상에서
최적조건은 A2
B3
C1
D1
E2
F3
G1
H3
이지만, 추정에는 큰 효과를 지닌 A, F, G, H만 사용하는데, 현행조건 A1
B2
C2
D2
E2
F2
G2 H2
와의 차이를 추정한다. F, G 는 현행수준과 마찬가지이므로 차이에 대해 이득을 부여하는
것은 A, H이다. 따라서 이득은
(
11.1 - 1.8 ) / 9 + ( 6.8 - 3.9 ) / 6 = 1.03 + 0.48 = 1.51 (dB)
이 된다.
SN비(η)의
이득과 표준편차는
σ2
= 10 (- η / 10)
(※)
의 관계식에서 η
= 1.51을 대입하면 σ
= 0.84 즉 현행조건보다 표준편차가 16% 감소한다.
손실은 1 - 0.842
= 0.294 즉 29.4% 감소한다.
dummy법은
직교표에서 열의 수준보다 적은 수준의 인자를 할당할 때의 수법이다. 조합법은 dummy법의
대상이 되는 인자가 복수개 있을 때 사용하는 방법이다. 예를 들면, 2수준의 인자가
A, B 2개 있을 때, dummy법이라면 3수준의 2열이 필요하지만, A, B의 4가지
조합가운데 다음 3가지만을 다루기로 한다면, 3수준의 열 1개로 가능하게 된다.
(AB)1
= A1B1
(AB)2
= A2B1
(AB)3
= A1B2
위의
(AB)를 조합인자라고 하며, 조합인자를 만들어 할당하는 방법을 조합법이라 한다.
A1과
A2의
비교는 (AB)1과
(AB)2로,
B1과
B2의
비교는 (AB)1과
(AB)3으로
할 수 있다.
조합법을 사용하면, 2수준의 2인자가 3수준의 1열에 할당하므로 극단적으로 말하면, 2수준의 15인자를 L18 에 할당할 수 있는 셈이 된다. 그러나 조합에 사용한 인자 상호간은 직교하지 않으므로 이제까지와 같이 전변동을 모든 요인변동으로 분해할 수는 없다. 따라서 조합법은 부득이한 사용방법으로 이해해야 한다.
예를 들면 A, B, C가 2수준, D, E, F, G, H, I가 3수준일 때 B, C에 dummy법을 사용하면 L18 에는 할당될 수없지만, 조합법을 적용하면 할당할 수 있는 경우에는 효과적인 것이다. 이 경우에도 AB를 조합시킬 것인가, AC를 조합시킬 것인가, 또는BC 를 조합시킬 것인가가 문제이다. 고유기술의 정보가 있는 한, 조합시키는 인자 가운데 적어도 한쪽은 효과가 별로 없는 것을 선택하는 것이 좋다.
한편
2수준의 A, B를 다음과 같이 조합하고 조합인자 (AB)의 각 수준에 r개씩의 반복이
있다고 하자. 만약 (AB)가 L18
의 3수준의 열에 할당되었다면, r은 6이다.
(AB)1
= A1B1
(AB)2
= A2B1
(AB)3
= A1B2
이때 조합인자 (AB)의 변동은
S(AB)
= { (AB)12
+ (AB)22
+ (AB)32
} / r - CT
(f
= 2)
이다. 이것은 AB의 3가지 조합간의 차이로 발생한 것이다. 분산분석에서는
하나 하나의 인자 효과의 크기로 분해하는 것이 중요하지만, 조합법을 사용한 A와
B는 직교하지 않으므로
S(AB)
= SA
+ SB
와
같이는 할 수 없다.
실제로
A가 제1수준인 실험은 (AB)1
(AB)3
이고 제2수준은 (AB)2
이지만 전자에는 B에 대해 B1
과 B2
가 있는데 반해 후자에는 B1
밖에 없다. 이래서는
{
(AB)1
+ (AB)3
} / 2 r - (AB)2
/ r = ( A1B1
+ A1B2
) / 2 r - A2B1
/ r
으로 하더라도 B에 대해 공평하지 않으므로 A의 비교라고는 할 수 없다.
그러므로 B가 고정된 조건에서 구하면 일단 A의 효과로서 생각할 수 있다. 이 경우
B가 고정되어 있고 A의 수준이 다른 것은 (AB)1
= A1B1
과 (AB)2
= A2B1
이다. 따라서 이 2수준의 차이는 A에 의한 것으로 생각할 수 있다. 즉 A의 변동은
SA
= { ( A1B1)2
+ ( A2B1)2
} / r - ( A1B1
+ A2B1)2
/ 2 r
또는
SA
= ( A1B1
- A2B1
)2
/ 2 r
으로 구한다. 이것은 B가 제1수준에 고정된 조건에서의 A의 효과의 크기이므로
B가 제2수준일 때도 성립되는지 여부는 알 수 없지만, 일단 A의 효과로 간주해 둔다.
B의
변동에 대해서도 마찬가지 방법으로 A의 수준이 고정되어 있고 B의 수준이 다른
(AB)1
= A1B1
과 (AB)3
= A1B2
에서
SB
= { ( A1B1)2
+ (A1B2)2}
/ r - (A1B1
+ A1B2)2
/ 2 r
또는,
SB
= ( A1B1
- A1B2
)2
/ 2 r
이다.
1) 4수준 작성방법
직교표 L8 에서 4수준의 열을 만들어 인자를 할당하는 방법을 알아본다.
A가 4수준, B, C, D, E가 각 2수준이라고 하자. 이들의 주효과를 L8 에서 구하려면 L8 (27 )가운데 4수준의 1열을 만들어야 한다. 4수준의 열을 2수준계의 직교표에서 만들려면 선점도 가운데 1개의 선분을 사용하면 된다. 예를 들면, L8 선점도의 삼각형의 1변 즉, 1열과 2열을 연결하는 선분을 생각한다. 그에 해당하는 3개의 열을 직교표 L8 에서 지우고 그 대신 4수준의 1열을 오른쪽 그림과 같이 만든다. 4수준의 1열은 그 선분의 양끝의 2열의 2수준, 1,2가 만드는 4가지 조합 (1 × 1), (1 × 2), (2 × 1), (2 × 2)에 대해 1, 2, 3, 4를 대입하여 4수준의 열을 만들고 그대신 3개 열을 지운다.
..gif)
할당은 표와 같다
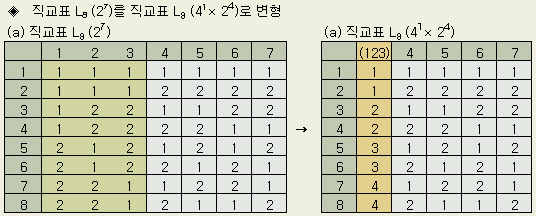
자유도 1인 3개 열을 없애고, 자유도 3인 4수준의 1열을 만든 것이 오른 쪽 직교표이다.
변동
SA의
계산
SA
= ( A12
+ A22
+ A32
+ A42
) / 2 - CT (f = 3)
2) 8수준 작성방법
2수준계 선점도에서 닫혀진 삼각형(삼각형에서 다시 하나의 꼭지점과 대변과의 교호작용을 추가한 것)을 사용함으로써 2수준의 7열(3개의 꼭지점, 3개의 변, 1개의 수직선)대신에 자유도 7인 8수준의 1열이 다음과 같이 들어가게 된다.
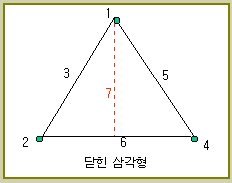
.gif)
L16
의 경우, 하나의 삼각형의 꼭지점 1에서 대변 6에 수직선을 내리면 7열이 된다. 즉,
점선 7 까지 추가한 그림과 같은 닫힌 삼각형의 3개의 꼭지점 1, 2, 4열의 8가지(23)
조합에 8수준의 인자를 넣는 것이다. 아래 표를 참조하시라.
이 경우 L16
가운데서 1, 2, 4열 외에 3, 5, 6, 7의 4열도 제거할 필요가 있다.
이렇게
L16(215)이
L16(81
× 28)으로
바뀐 새 직교표는 다음과 같다.
직교표 L16(215)에서 만든 직교표 L16(81 × 28)
_ortho.gif)
3) 3수준계에서 9수준의 열을 만드는 방법
3수준계의 선점도 가운데 1개의 선분을 이용하여 9수준의 열을 만들 수 있다. 예를 들면 L27(313)가운데 임의의 1개의 선분을 만들기 위해 2열과 5열을 선택한다면, 교호작용이 나타나는 열은 8, 11열이 된다. 양끝 2열과 5열의 수준1, 2, 3의 조합 (11), (12), (13), (21), (22), (23), (31), (32), (33)에 1, 2, 3, 4, 5, 6, 7, 8, 9을 대입하여 9수준을 넣은 새 열이 만들어지고, 2, 5, 8, 11열을 표로부터 없앤다.
_ortho.gif)
물론
9개 수준열이라고 해서 반드시 9개 수준을 넣을 필요는 없고, 4~8개 수준을 넣는
경우는 앞절의
dummy법으로 처리하면 된다
4) 혼합계
직교표 L18에서
다수준 열을 만드는 방법
교호작용의 열이 구분되지 않는 혼합계 직교표에서는 다수준 열을 만들 수 없으나,
오직 L18의
1열과 2열의 조합으로 6수준의 다수준을 만들 수 있다. 2열과 3열의 수준의
조합 즉,
(11),
(12), (13), (21), (22), (23)의 새로운 열을 만들고 대신 1열과 2열은 없애야 한다.
만약 필요한 수준이 4 혹은 5라면 앞절의 dummy법으로 처리하면 된다.
의인자법(擬因子法)은 여러가지 요인을 하나의 직교표에 할당할 경우에 유용한 수법으로, 어떤 인자의 수준에 따라 별도 인자의 조를 실험하고자 하는 경우의 변신법(變身法)과 3수준, 5수준, 7수준등의 인자를 2수준계의 직교표에 할당하거나 7수준을 3수준계의 직교표에 할당하는 유휴열법(遊休列法)이 있다. (유휴열법은 생략함)
< 변신법>
양복을
만드는 작업에서 안감대는 방법으로
A1
: 깁는 방법
A2
: 접착에 의한 방법
가운데 어느 쪽이 좋은지를 비교해 본다.
A1 : 깁는 방법의 경우에 문제가 되는 인자에는
B’
: 실의 종류
2수준
C’
: 깁는 방법
2수준
이 있으며
A2
: 접착에 의한 방법인 경우에는
B’’
: 접착제의 종류 2수준
C’’
: 접착방법 2수준
을 택하고자 한다. 즉 A의 수준에
따라 연구하고자 하는 인자가 서로 다르다. 변신법은 이같은 경우의 할당방법이다.
이밖에 어느 쪽이나 공통되는 인자로서 2수준의 D와 E가 있다.
<이 문제의 설명은 생략하고, 직교표의 배치를 보인다>.
.gif)
< 변신법의 실험예 (공구의 절삭성)>
1) 인자와 수준
미소 절삭영역에서 설정 절삭깊이의 치수 정밀도를 SN비로 검토하기 위해 공구 및 절삭기구 부착조건, 공구형상, 절삭조건을 다루었다.
공구는 초경(超硬)공구, 소결(燒結) 다이아몬드 공구, 천연 다이아몬드 공구가 있지만, 천연 다이아몬드 공구는 이미 연마되어 있으며 절삭기구 조건, 공구형상을 바꿀 수는 없다. 따라서 절삭기구 부착조건, 공구형상은 천연 다이아몬드 공구에서는 연구의 대상이 되지 않으며 이들은 초경공구, 소결 다이아몬드 공구에 대한 인자이다.
여기서
공구를
2그룹으로 나누어
A1
: 절삭기구 부착등이 필요한 초경공구, 소결다이아몬드 공구
A2
: 천연 다이아몬드 공구
다음에
초경공구,
소결 다이아몬드 공구를 비교하기 위해 A1
만의 인자 B를
B1
: 초경공구
B2
: 소결 다이아몬드 공구
로 한다. 이밖에 A1
만의 인자로서
C
: 공구 연마 지석(砥石) 4수준
D
: 공구 작동각도
2수준
E
: 공구 어프로치 각도 2수준
이 있다.
그리고
절삭조건은 A1
A2에
공통되는 인자로서 여기서는
F
: 절삭속도
2수준
G
: 이송
2수준
이다.
이상은
내측인자이며,
SN비를 구하기 위한 외측인자로서는 신호인자 M으로 하여 절삭깊이를 3수준 M1
: 5 (μm) M2
: 25 (μm) M3
: 50 (μm)
오차인자는
실내환경
I, 측정방향 J를
I1
: 공기조절 있음
I2
: 공기조절 없음
J1
: X방향
J2
: Y방향
으로
했다.
그리고 피삭재는 알미늄이다.
2) 할당과 SN비
인자 B에서는 E는 A1 만의 인자이므로 변신법으로 할당한다. A의 수준에 따라 어떤 인자를 선별 사용하려면, A와의 교호작용의 열이 필요하다. 이 경우 A와 B, A와 C, A와 D, A와 E의 교호작용을 확보해야 한다. B는 4수준이므로 다수준 작성법을 적용한다. 이들 구하고자 하는 정보를 선점도로 표시하면 그림과 같이 된다
..gif)
이것을 요구되는 선점도라 한다.
이 도형에서 필요한 자유도는 15이므로 직교표로서는 L16 을 사용하기로 한다. L16 의 선점도를 다음 그림 같이 변형하여 요구되는 선점도에 열번호를 대응시킨다.
.gif)
이상에서 표와 같이 할당되었다.
.gif)
3) 외측 데이터에 의한 SN비
직교표의 실험번호별로 시험편에 대해 절삭깊이를 바꾸어 직경방향 X, Y의 실질 절삭량을, I1 : 공기조절 있음, I2 : 공기조절 없음의 2조건으로 측정했다. no. 1의 데이터는 표와 같다.
.gif)
비례식에 의해 SN비를 구한다.
ST
= 0.32
+ 0.252
+ … + 4.52
= 103.23 (f = 12)
Sβ
= ( 0.5 × 1.05 + 2.5 × 8.55 + 5 × 18.4 )2
/ { 4 × ( 0.52
+ 2.52
+ 52
) }
= 102.96 (f = 1)
Se
= 0.027 (f = 11)
Ve
= 0.027 / 11 =0.0245
η
= {
( Sβ
- Ve
) / r} / Ve
=
10 log { ( 102.96 - 0.0245 ) / ( 4 × ( 0.52
+ 2.52
+ 52
) × 0.0245 ) }
= 15.2
(dB)
이와 마찬가지로 하여 앞에서의 SN비 난이 계산된다.
4) 분산분석
보조표로서
수준별 합계표를 만든다.
B부터 E는 A1
일 때만의 인자이므로, A의 열이 제1수준의 실험번호로부터 수준별 합계를 만들게
된다. 앞의 양복 만드는 작업일 경우에는 A1
과 A2
간에 서로 다른 인자를 선택했지만, 여기서는 A2
의 경우 B부터 E에 대응하는 인자가 없다. 여기서는 오차가 구해지므로, 검산을 위해서는
A의 열이 제2수준일 때 B, C, D, E의 열에 대한 수준별 합계도 만들어둔다.
.gif)
변동의
계산은 다음과 같이 한다.
ST
= 15.22
+ 15.22
+ … + 22.72 -
332.22
/ 16 = 187.42 (f = 15)
SA
= ( A1
- A2
)2
/ 16 = ( 145.0 - 187.2 )2
/ 16 = 111.30 (f = 1)
다음에
SB,
SC,
SD,
SE
는 A1
일 때만의 데이터로부터 구한다.
SB
= ( B - B )2
/ 8 = ( 68.1 - 76.9 )2
/ 8 = 9.68 (f = 1)
SC
= ( C12
+ C22
+ C32
+ C42
) / Ci의
반복수 - A12
/ 8
= ( 30.42
+ 34.92
+ 36.32
+ 43.42
) / 2 - 145.02
/ 8
= 43.59 (f = 3)
SD
= ( D1
- D2
)2
/ 8 = 3.65 (f = 1)
SE
= ( E1
- E2
)2
/ 8 = 0.84 (f = 1)
SF
SG는
전체의 데이터에서
SF
= ( F1
- F2
)2
/ 16 = ( 164.8 - 167.4 )2
/ 16 = 0.42 (f = 1)
SG
= 1.10 (f = 1)
이
된다.
Se
는 ST
에서 빼면
Se
= ST
- ( SA
+ SB
+ SC
+ SD
+ SE
+ SF
+ SG
)
= 16.84 (f
= 6)
이것은 B, C, D, E의 할당열에 대응하는 A2 만일 때에 4가지 변동의 합이 될 것이므로 검산해 보자.
S
2열4열6열
= ( 46.02
+ 50.72
+ 44.32
+ 46.22
) / 2 - 187.22
/ 8
= 11.23 (f
= 3)
S
8열
= ( 96.9 - 90.3 )2
/ 8 = 5.44 (f = 1)
S 10열
= 0.08 (f = 1)
S 12열
= 0.08 (f = 1)
이상에서
Se
= S2열4열6열
+ S 8열
+ S 10열
+ S 12열
= 16.83
0.01의 차이는 숫자를 정리하는데 따른 오차에 의한 것이다.
분산분석표로
정리하면 표와 같이 된다..gif)
오차분산보다 작은 요인과 오차분산 정도의 요인을 pool하고 (e)를 만들었다.
기여율은
ρA
= { SA
- fA
V(e)
} / ST
× 100 = { ( 111.30 - 1 × 2.28 ) / 187.42 } × 100 = 58.2
(%)
ρB
= { SB
- fB
V(e)
} / ST
× 100 = { ( 9.68 - 1 × 2.28 ) / 187.42 } × 100 = 3.9
(%)
ρC =
{ SC
- f C
V(e)
} / ST
× 100 = { ( 43.59 - 3 × 2.28 ) / 187.42 } × 100 = 19.6
(%)
ρ(e)
= { S(e)
+ ( fA
+ fB
+ fC
) × V(e)
} / ST
× 100
= { 22.85 + 5 × 2.28 } / 187.42 × 100 = 18.3
(%)
5) 추정
효과가
큰 요인은
A, B, C이고 각 평균값은 다음과 같다.
A1
= 145.0 / 8 = 18.125
A2
= 187.2 / 8 = 23.4
B1
= 68.1 / 4 = 17.025
B2
= 76.9 / 4 = 19.225
C1
= 30.4 / 2 = 15.2
C2
= 34.9 / 2 = 17.42
C3
= 36.3 / 2 = 18.15
C4
= 43.4 / 4 = 21.7
A1 A2 의 비교에서 A2 쪽이 좋은 것처럼 보이지만, A1 A2 의 우열은 각각의 최적조건 상호간을 비교하고 결정해야 한다. A2 는 A2 고유의 인자는 아니므로 이런 상태라도 좋다. A1 은 B2 C4 D1 E1 이 최적조건이다. 이 가운데 효과가 큰 것은 B, C이므로
μ(A1
B2
C4)
= A1
+ ( B2
- A1
) +
( C4
- A1
) =
B2
+ C4
- A1
= 19.225 + 21.7 - 18.125 = 22.8
(dB)
이
된다.
이 결과에서 A2
는 A1
B2
C4
보다 약간 좋지만, 거의 차이는 없다고 할 수 있다. 즉, 소결 다이아몬드라도 연마지석의
선택에 따라 가장 예리한 천연 다이아몬드 공구과 같은 정도의 가공성을 지닌다고
할 수 있다.