|
제4편 사례 2장 망목특성 |
|
2.1 실험조건과
직교표 할당 2.2
SN비와
감도 계산 2.3 SN비의 변동계산 2.4 SN비의 분산 분석 2.5
감도의
분산분석 2.6
목표치에의
조정 2.7 최적 조건 |
특정의
목표치가 있고, 아래 위의 허용폭이 정해지는 망목특성은, 먼저 안정성(robustness)의
개선을 한 상태에서, 목표하는 특성치를 맞추는 2단계 작업으로 데이터 해석을
실시한다.
<1장 망소특성>의 사례를 먼저 보신 전제로 설명한다.
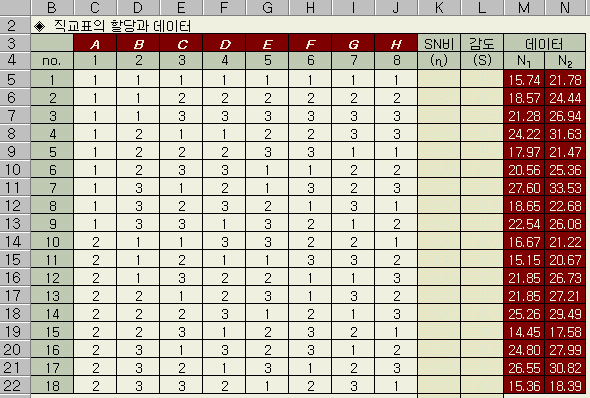
video tape의 back tension 조정부의 최적화를 위해, 다음과 같은 제어 인자를 채택하고, 이론식으로 계산을 했다. 이 back tension 조정 기구에서는, tape의 감긴 상태가 바뀌어도 tape tension이 변하지 않고, 일정(24.5 g)하게 유지됨이 이상적이다.
실험조건과
얻어진 데이터는 아래와 같다.


望目特性의 경우, SN비와 感度에 대해 각각 분산 분석을 하여 유의한 인자를 찾고, 이에 의하여 공정 평균을 구하고 최적 조건을 결정한다. SN비는 안정성의 척도이며, 감도는 출력을 목표치에 조정하기 위해 필요하다.
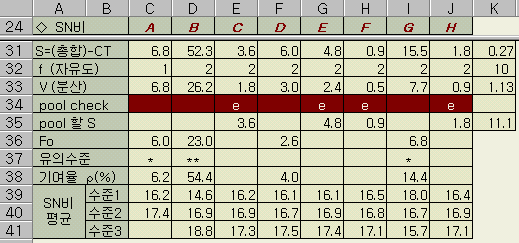
2 .2 SN비와 감도 계산
위와 같은 데이터가 얻어지면, 실제적인 계산은 Excel과 같은 spread sheet 프로그램으로 할 것이다. (망소특성과 중복되는 내용은 설명을 생략한다)
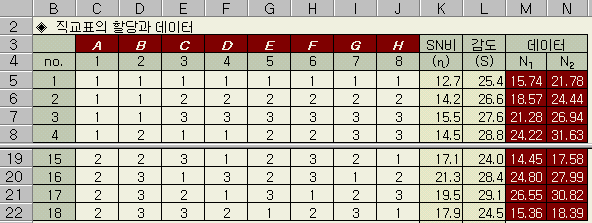
실험 no. 1에 대한 계산
◈ SN비 η
= 10 log ( m2 / σ2
)
= 10 log [ { ( Sm
-
Ve
) / n}
/ Ve]
K5
= 10 * LOG (
( SUM (M5:N5)^2 / 2
- VAR
(M5:N5) ) / 2
/ (VAR
(M5:N5) ) )
= 12.7
◈ 감도
S = 10 log {(Sm
-
Ve
) / n}
L5
= 10 * LOG ( ( SUM (M5:N5)^2
/ 2 - VAR
(M5:N5)
) / 2 )
= 25.4
no. 2 ~ 18 의 계산은 위의 식을 입력한 K5:L5셀을 나머지 셀에 복사하면 된다.
(계산식에 대해서는 <제2편 1장 손실함수와 SN비>를 참조)
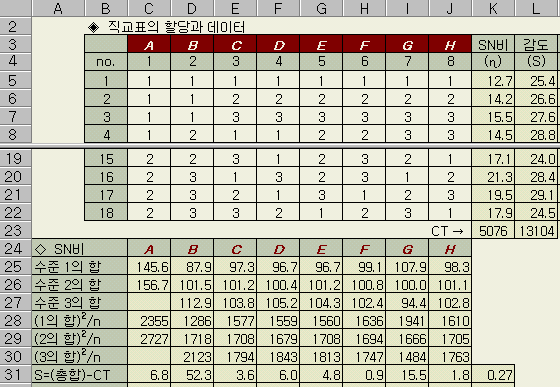
◈
수준
1의
합
D25 = SUMIF ( D$5:D$22, 1, $K$5:$K$22 ) = 87.9
수준
2의
합
D26 = SUMIF ( D$5:D$22, 2, $K$5:$K$22 ) = 101.5
수준
3의
합 D27
= SUMIF ( D$5:D$22, 3, $K$5:$K$22 ) = 112.9
◈
변동 (S)
D31 = ( D25^2 + D26^2 + D27^2 ) / 6 - $K23(CT)
= SUMSQ ( D25:D27 ) / 6 - $K23 = 52.3
※ 2수준 열인 A인자의 경우, 실험회수 n = 9 자유도(f) = 1에 유의할 것
◈
수정항(CT)
SN비
K23
= SUM ( K5:K22 )^2 / 18 = 5076
감
도
L23
= SUM ( L5:L22 )^2 / 18 = 13104
◈
V (분산) VB
= 변동 / 자유도
D33
= D31 / D32 = 26.2
◈
pool check
V(분산:33행)가 오차분산과 비슷하거나 작은 인자를 오차로 pooling하기
위하여 34행에 'e'를 입력하면 그에 해당하는 변동(S)이 35행에 나타나고 K열에 합계가
된다. 오차가 배치되지 않은 경우에는 V값이
작은 몇개로 pooling한다.
◈
F0 (분산비) F0 = V / V(e)
D36
= IF (ISTEXT (D34),"",D33/$K33)
= 23.0
(ISTEXT는
31행에서 'e'로 오차처리한 인자는 33행을 비게하기 위함)
◈ 유의수준
33행의 F0값을
F분포의 값으로 검정하여 유의여부를 표시
D37
= IF (ISNUMBER (D36), IF(D36 > FINV
(0.01,D32,$K32)
,"**",IF
(D36 > FINV (0.05,D32,$K32), "*", "") ) , ""
)
◈ 기여율 ρ
D38
= IF (ISTEXT (D34), "" ,
(D31-(D32*$K33) ) *100/DEVSQ ($K5:$K22) )
=
54.4
※
K31~K35의 4셀은 오차분산 V(e)를 계산한다. 위 표의 계산에서 숨겨져
있는 1,2 열의 교호작용 효과(변동과 자유도)에 유의할 것.
K31
= DEVSQ (K5:K22) - SUM (C31:J31) =
0.27
(∵
1열과 2열 교호작용 변동 = 총변동(ST) - 각 인자의 변동 합계)
K32
= 17 - SUMIF ( C34:J34, "",
C32:J32 ) = 10
pooling된
오차분산의 자유도 (1,2열의 교호작용 자유도 2에 유의)
K33
= ( K35 + K31 ) / K32
= 1.13
오차분산 V(e)
C34~J34 : C33~J33의
분산으로 pooling할 인자와 본디 오차열에 'e'표시
K35 = SUM (C35:J35)
= 11.1
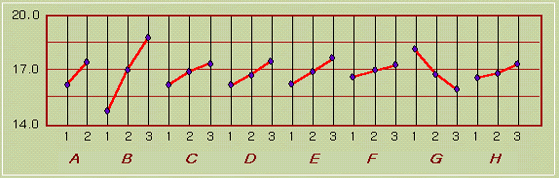
◈
요인
효과도 (SN비)
감도의 변동계산과 분산분석은 SN비의 그것과 같으므로 설명을 생략함
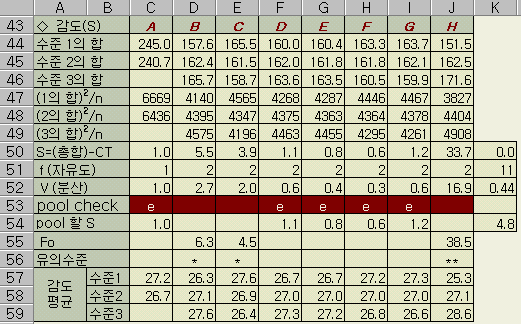
◈ 요인 효과도 (감도)
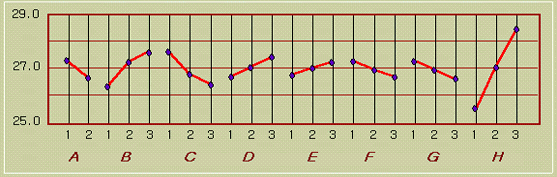
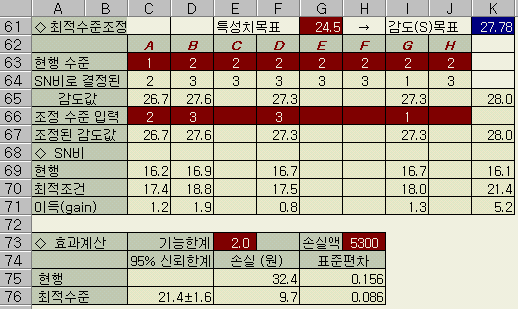
望目特性의 경우 처음은 목표치를 생각하지 않고 SN비의 최적조건을 찾는다. (望小와 望大特性은 이런 문제가 아예 없다. SN비가 큰 값만을 선정하면 된다)
SN비의 최적 조건은 요인 효과도나 SN비의 평균(36~38행)으로 부터, A2 B3 C3 D3 E3 F3 G1 H3 인 것을 알 수 있으나 오차에 pooling한 인자와 분산분석에서 유의하지 않은 인자는 제외시키면 A2 B3 G1 이 채택조건이다.
이 조건에서 특성치가 목표치와 일치할 가능성은 작다. 차이가 있을 때의 조정은 다음의 순서에 따른다.
①
특성치목표
m(G55)에 대한 감도값(K55)을 구한다.
S
= 10 × log m2
= 10 log 24.52
= 27.78
②
SN비에서
유리한 수준(58행)중에서 오차로 pool한 인자를 제외한 인자의 감도값(59행)과 그
합계가 K59이다.
예상감도(K59)
= 26.7 + 27.6 + 27.3 + 27.3 - 3 × (18회 실험의 감도평균) = 28.0
그러나
59행에 기입된 인자가 현행조건보다 최적조건이 유리한 인자를 나타내는 것은 아니다.
인자별 효과는 65행에 나타나며, 최적조건에서의 개선효과를 계산하려면 여기서 큰
인자만을 선정(60행에 입력)할 필요가 있다.
③
감도목표치(K55)와
K59를 비교하여 조정할 인자수준을 60행에 입력하면 61행에 그에 해당하는 감도값이
나타나며 K61에서 최종적인 감도값을 확인할 수 있다.
60행의
수준입력은 SN비에는 영향없되 감도에는 유의한 인자가 우선적으로 선정되며, 최종적으로
SN비를 저해하면서 특성치의 목표에 맞추려는 경우는 F69와
F70의 손실의 차이를 최대화하는 조건을 찾아야 한다.
망소특성이나 망대특성에서는 효과있는 인자의 수준만 확정되면 나머지 인자의 수준은 SN비가 유리하거나 경제적인 인자를 선택하면 되지만, 망목특성의 경우에는 평균치나 SN비에 영향을 미치는 등 복잡하므로 대부분 인자의 수준을 선정해야 할 것이다.
註
: 특성의 목표치로 맞추는 인자를 조정인자라 한다. 조정인자는 실험결과가 나오기
전에는 알 수 없고, 위와 같은 계산을 거친 후 확인되는 것이다.
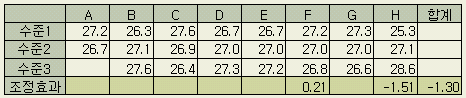
註 : 앞에서 최적조건의 감도를 모든 채택인자에 대해서 계산하였으나 특성치(감도)에 영향을 미치는 것은 감도의 분산 분석표에서 효과가 큰 인자인 것이다. 그래서 효과가 큰 3개의 요인 B, C, H의 SN비 채택수준에 따라 다음과 같이 계산해도 좋다.
S
= B3
+ C3
+ H3- 2
× T
= 27.61+26.45+28.60-2
× 26.98=28.70
(dB)
<A2>
<B3>
C3
<D3>
E3
(F2)
<G1>
(H2)
위의
인자별 수준중 괄호 <
>는 SN비에서 유의한 수준이고, ( )는 목표치의 조정을 위해서 필수적으로
채택되어야 하는 수준이며, 나머지는 경제성에서 불리함이 없으면 나쁘지 않는
(좋다고는 판정이 되지 않은) 조건이다.
최적 조건의 SN비의 추정은, 분산 분석표(SN비)로부터, 효과가 큰4개의 요인을 선택하고 계산을 하는 경우,
μ
= A2
+ B3
+ D3
+ G1
- (3 × T)
=
17.4+18.8+17.5+18.0-(3
× 16.8)
=
21.4
(dB)
이
된다.
註 : SN비의 값 (여기서 21.4)은 절대값으로 아무 의미도 주지 않는다. 즉 상대적으로 비교할 때 의미를 가진다. 이득(gain) 값은 산포증감의 효과를 알려준다.