|
제4편 사례 3장 동특성 |
|
3.1
실험의
내용 3.2
인자와
직교표의 할당 3.3 변동과 SN비의 계산 3.4
분산분석 3.5 확인실험과 개선효과 |
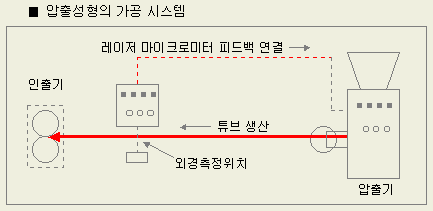
자동차 wire harness 조립부품의 하나인 서모플라스틱(thermo- plastic) 압출 성형품의 산포는 후공정에서 여러 가지로 문제를 일으킨다. 플라스틱 튜브의 외경이 압출 스크루의 회전수 변화에 보다 민감하게 작동되며, 더욱 산포가 작고 원활하게 조절할 수 있는 조건를 구하는 것이 이 실험의 목적이다.

생산된 튜브의 외경이 헬륨 - 네온 레이저에 의해 측정되며, 이 값이 압출기의 제어시스템으로 피드백되어 스크루 회전수를 제어한다. 이와 같이 순간순간 변화되는 입력(신호인자)에 연동되어 적절한 결과를 얻고자 할 때의 경우가 동특성의 실험에 해당한다.
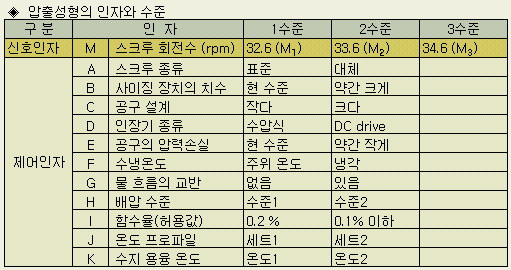
제어인자는
다음과 같은
11개 인자를 선정하여 L12
직교표에 할당하였다.
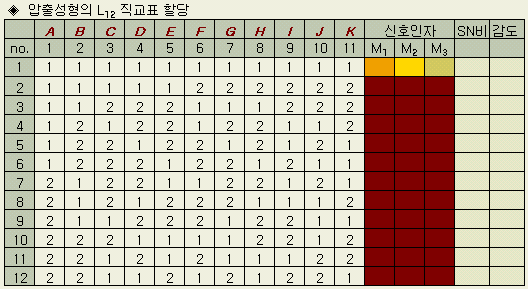
직교표 할당에서 보는 것과
같이 특별한 오차인자를 다루지 않았는데 다음과 같은 이유에서이다
. 즉 실험시간이 1일 8시간으로 2일이 걸리며, 그 시간 동안에 다음과 같은 변화가
실험에 포함되므로 적절한 오차가 포함되어 있다고 볼 수 있다.
①
온도변화가 20℃가 된다.
②
여러 가지 예기치 못한 지연이 발생한다.
③
공구 설정의 산포가 생긴다.
신호인자의 각 수준에 대해
12개의 데이터를 취했다. 신호인자가 3수준이므로 합계 36개의 데이터이다. (앞의
표에 표시된 색상과 아래 데이터의 관계를 이해하시라)
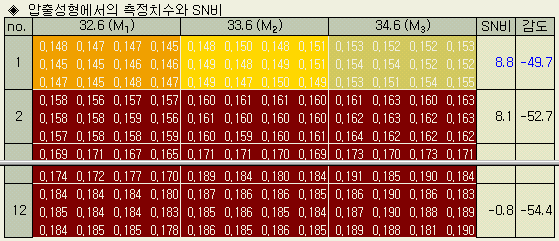
no.1에서의
전변동 (ST), 비례항 변동 (Sβ),
오차변동 (Se)
과 SN비 (η)의 계산을 보인다.
◈ ST
= 0.1482
+ 0.1452
+ 0.1472
+ … + 0.1522
+ 0.1552
- (no.1의 36개 합)2
/ 36
= 0.8043200 - (5.38)2
/ 36 = 0.0003088889
◈ Sβ
= { ( M1
- MM ) × y1
+ ( M2
- MM ) × y2
+ ( M3
- MM ) × y3
}2
/ r
여기서 M1
= 32.6 M2
= 33.6 M3
= 34.6이며 MM은 이들 3개의 평균치를 나타낸다.
y1
= M1
조건의 12개 데이터의 합 = 0.148 + 0.145 + … + 0.147 = 1.756
y2
= M2
조건의 12개 데이터의 합 = 0.148 + 0.148 + … + 0.149 = 1.789
y3
= M3 조건의
12개 데이터의 합 = 0.153 + 0.154 + … + 0.155 = 1.835
r = r0
{ ( M1
- MM )2
+ ( M2
- MM )2
+ … + ( Mk
- MM )2
}
= 12 { (32.6 - 33.6)2
+ (33.6 - 33.6)2
+ (34.6 - 33.6)2
}
= 12 { (-1)2
+ 02
+ 12}
= 24
∴ Sβ
= { (32.6 - 33.6) ×1.756 + (33.6 - 33.6) ×1.789 + (34.6 - 33.6)
×1.835 }2 / 24
=
0.0002600417
◈ Se
= ST
- Sβ
= 0.0000488472
Ve
= Se
/ ( k r0
- 2) = 0.0000488472 / (3 × 12 - 2) = 0.0000014367
◈ η
= {(Sβ
- Ve
) / r} / Ve
= { (0.0002600417 - 0.0000014367)
/ 24 } / 0.0000014367 = 7.50006
= 10 log (7.50006) = 8.8
(dB)
◈ 감도(S) = (Sβ
- Ve
) / r
=
(0.0002600417 - 0.0000014367) / 24 = 0.000010775
= 10 log (0.000010775) = -
49.7 (dB)
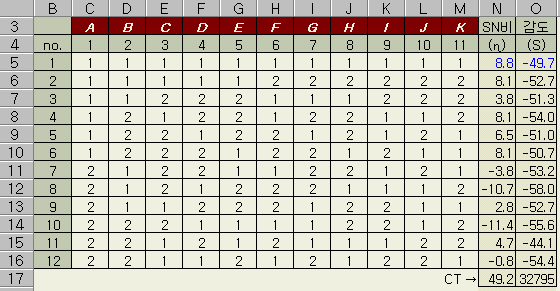
나머지 no.2 ~ no.12도 마찬가지로 계산하여 위표에 정리하였다. (Exel로 계산하면 부담스럽지 않다)
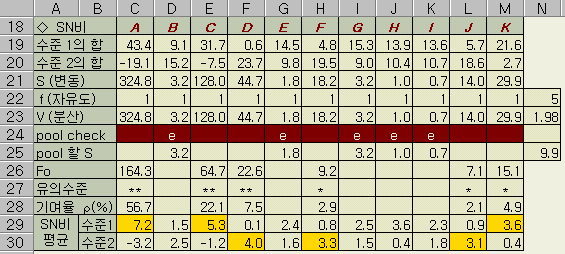
23행의
분산 (V)이 작은 인자를 pooling하기 위하여 24행에서 e로 첵크하였다. 계산된 분산분석표에서
기여율이 높은 반수정도의 인자를 택하고, SN비가 큰 수준의 조합으로 최적조건을
구한다. 표에서 주황색의 수준이 그것이다. 최적조건의 추정치는
η = A1
C1 D2 F2 J2 K1 - (5 ×
T)
= 7.2 + 5.3 + 4.0 + 3.3 + 3.1 + 3.6 - (5 × 2.0) = 26.5 - 10.0 = 16.5 (dB)
註 : 평균값이 2.0 dB임에도 11가지라는 많은 인자를 포함시킨 실험 결과에서 양호한 수준들을 취합 함으로써 16.5 dB 이라는 높은 값을 구할 수 있는데서 직교표 실험의 위력(?)을 실감할 수 있겠다.

최적조건으로 재현 실험을 한 데이터는 위와 같으며, 추정한 SN비에서 3 dB이내이면 실험결과는 재현성이 있는 것으로 본다
튜브의
외경은 망목특성이다
. 이 실험전 8개월에 걸친 50개의 시료를 측정한 값은 평균이 0.150013, 표준편차
(σ) 가 0.001376이었다.
튜브의 규격은 0.150 ± 0.003 inch, 튜브의 폐기비용 A는 12인치 길이당 0.0191$
이다. 손실함수 L은
L =
A / Δ2
× [σ2
+ (평균 - 목표값)2
]
이므로
L = 0.0191
/ 0.0032 × [ 0.0013762 + ( 0.150013 - 0.150 )2
]
= 0.0040
($ / 개)
확인실험후 스크루 회전수의 제어회로를 튜브외경이 0.150 inch가 되도록 정비하였다. 최적조건으로 50개의 시료를 측정하여 평균값 = 0.149880, 표준편차 = 0.000773 이 얻어졌다. 따라서 수정후 손실함수 L은
L = 0.0191
/ 0.0032
× [ 0.0007732
+ ( 0.149880 - 0.150 )2
]
= 0.0013
($ / 개)
즉 손실의 70%를 개선하는 효과가 있다.