a1X1 + a2X2 + … + a10X10
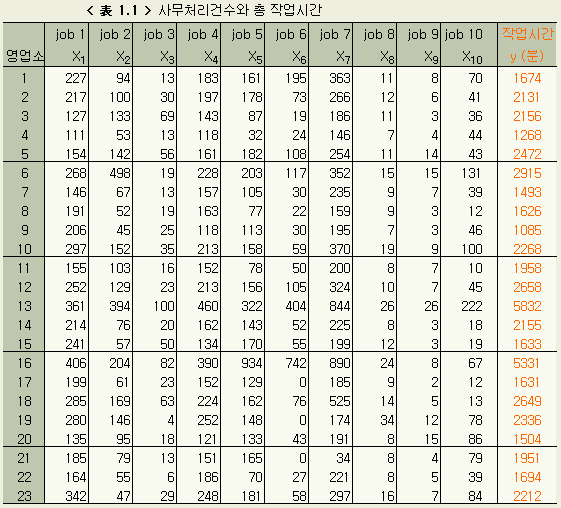
로 나타낼 수 있다. 그런데, 전국의 영업소중 적당한 23개소를 뽑아, 각각의 영업소에서의 작업건수 X1, X2, …, X10 과 그 날의 각 영업소에서의 작업시간 y 를 조사한 것이 < 表 1.1 > 이다.
|
제5편 Simulation 1장 실험적 회귀분석의 기초 (이미 확보된 자료에 의한) |
|
①직교표,
②檢定과 분산분석, ③엑셀의 구사(驅使) 가 완전한 이해를 위한
先修과정이지만, 본문을 精讀하며 아래의 엑셀파일을 이용하면 문제의
풀이는 가능할 것입니다. ◈ 응용을 위한 몇가지 사례를 소개합니다. → 활용사례 |
|
1.1 개요 1.2 최소제곱법 적용의 문제점 1.3 실험적 회귀분석의 방법 2) 직교표에 의한 계산 2.3 사무작업분석의 경우 |
1.1 개요
지금 어떤 회사의 사무작업을 분석하려고 한다. 이 회사에는 전국에 100 개 이상의 영업소가 있고, 각 영업소의 주요한 작업은 10 種이다. 물론 각 영업소별로 10 종의 작업량과 그 구성비도 다르다.
지금 10 종의 작업
발생건수를 X1, X2, …, X10 으로 하여, 각각의
한 건당의 표준시간을 a1, a2, ..., a10
로 하면, X1, X2, …, X10 업무에
소요되는 시간은
a1X1
+ a2X2 + … + a10X10
로
나타낼 수 있다. 그런데, 전국의 영업소중 적당한 23개소를 뽑아, 각각의 영업소에서의
작업건수 X1, X2, …, X10 과 그 날의 각
영업소에서의 작업시간 y 를 조사한 것이 < 表 1.1 > 이다. 
이 때 작업시간 y와
작업량 X1, X2, …, X10 과의
관계식은
y
= m + a1X1 + a2X2 + … + a10X10
(1.1
)
이다. 이와 같은
관계식을, y를 목적변수, X1, X2, ...,
X10 을 설명변수로
하는 미지수 a1, a2, ..., a10 에 대한
1차회귀식이라고
한다. 여기서 m은 10종류의 작업 이외에 소요된 시간으로, 여유시간과 기타의 시간이포함된다.
< 表 1.1 > 의 데이터로 식 (1.1 ) 의 m, a1, a2, ..., a10 을 추정하려는 것이 여기서의 과제이다.
사무작업이라는 것은 하나하나의 일의 매듭이 명확하지 않거나, 그 처리시간의 불규칙하고 산포도 커서, 스톱워치 등으로 시간관측을 하기도 하고, 요소작업으로 분해하여 표준시간 a1, a2, ..., a10 을 높은 精度로 구하기 위해서는 많은 관측이 필요로 한다. 이 경우의 일반적 해법이 重回歸분석이며, 최소제곱법이 그 기본적인 원리이다.
< 表 1.1 >의
데이터에 최소제곱법을 적용하면 다음의 결과를 얻는다.
y
= - 35.2 - 1.2 X1 + 2.0 X2 + 11.2 X3 +
12.7 X4 + 1.3 X5 + 0.7 X6
-
1.7 X7 - 22.6 X8 + 20.4 X9 - 3.0
X10 (1.2
)
즉,
m = - 35.2
a1 =
- 1.2
a2 =
2.0
a3
= 11.2
……
a10 =
- 3.0
이다.
|
◈ 최소제곱법에 의한 회귀분석 |
|
|
이 결과 여기에는 다음과 같은 문제점이 있음을 알수 있다.
즉 m, a1, a2, ..., a10 의 값을 실제적인 표준시간으로 생각할 수 없다. 왜냐면 표준시간으로서 m = - 35.2 (분), a1 = -1.2 (분) ... 이라는 마이너스 값은 있을 수 없기 때문이고, X1 만이 現狀보다 작업량이 증가하는 경우, 식 (1.2 ) 에 의하면 소요시간 y 가 도리어 줄어들게 된다.
이와 같은 불합리는 최소제곱법을 쓰면 당연히 나타날 수 있는 것이다. 최소제곱법은 미지수 m, a1, a2, ..., a10 이 구간 [-∞, +∞]의 모든 값을 취할 수 있다는 전제하에서 계산하는 것이다.
또한 X1 이 크면 X2 도 크다든지 하는 X1, X2, ..., X10 간의 상관성이 있는 경우도 많다. 이런 경우에 최소제곱법을 적용하면 미지수 m, a1, a2, ..., a10 의 추정精度가 좋지 않거나, 올바른 표준시간과는 거리가 먼 결과를 얻게된다. 올바른 계수를 구하는 경우에 최소제곱법을 쓰는 것은 애시당초 무리라고 할 수 있다.
위와 같은 결점을
없애기 위해서는 다음 사항을 고려한 방법을 생각해야 된다.
①
미지수( 계수)에 현실적으로 타당한 제한 범위를 설정하고, 그 범위내에서 잘 맞는
式을 찾는다.
② 찾는 방법으로서는 검정과 축차근사(逐次近似)를
반복함으로 계수의 폭을 단계적으로 좁혀간다.
③ 최종적으로
좁혀진 계수의 범위에 의하여 식의 계수를 결정하기 위해서는 실제의 작업을 잘 알고
있는 사람의 의견을 중시한다.
이러한 요구를 충족하는
방법의 하나가, 이 장에서 설명하려는 실험적
회귀분석이다. (simulation에
의한 회귀분석) 전문적인 프로그램도 있겠지만, 여기서는 엑셀에 의한 계산을
보인다. (계산의 조작이 쉽지 않다고 느낄 수도 있겠지만)
함수형은 식 (1.1)
에서와 같이
y
= m + a1X1 + a2X2 + … + a10X10
이다.
m, a1, a2, ..., a10 의
추정을 최소제곱법이 아닌, 실험적(simulation)으로 구하려는 것이다.
먼저 a1, a2, ..., a10 을 각각의 작업의 한 단위(일의 건수나 전표의 매수 등) 증가될 때마다 작업시간 y 에 영향을 미치는 시간, 바꾸어 말하면 각 작업의 표준시간과 같은 값의 대체적인 범위를 상정하여, 그 범위내에서 원칙적으로 등간격의 3수준을 만든다. 예를 들면 job 1의 작업 1건에 소요시간이 최대 8분이라고 한다면, 미지수 a1에 대해서 다음의 3 수준을 만든다. 즉
a1의
제1수준 : a11 = 0 분
a1의
제2수준 : a12 = 4 분
a1의
제3수준 : a13 = 8 분
이다. 이것을 a1
에 대한 초기값으로 한다.
이 경우, 범위는
정확하고 좁을수록 좋기는 한데, 그렇다고 수준값이나 폭에 대해 너무 신경과민일
필요는 없다 (지나치게 벗어나지만 않으면 자체적으로 답을 찾아주기 때문에). job
2 이하에 대해서도 마찬가지로 a2, a3, ..., a10 의
범위를 고려하여, 각 수준값을 설정한다. 이들을 종합한 것이 < 表 1.2 > 이다.
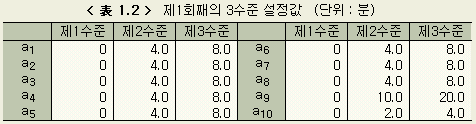
지금 a1,
a2, ..., a10 이 모두 제2수준으로서 작업량 X1,
X2, , …, X10 이 < 表 1.1 > 의 No.1의 영업소와 같았다고
한다면, No.1의 영업소의 작업시간 ý1
(추정치 표기를 이렇게 하자. 본디는
^ 표기로 하지만)은
ý1
= m + a1X1 + a2X2 + … +
a10X10
=
m + 4.0 × 227 + 4.0 × 94 + … + 2.0 × 70 =
m + 5254 (분) (1.3
)
이 되었을 것이다. 그런데 No.1 영업소의 실제 작업시간은 1674 분이었으므로
y1 - ý1
은 실제의 걸린시간과 한 단위당의 시간을 a1
= 4.0 (분), a2
= 4.0 (분), …, a10
= 2.0 (분)으로 가정해서 계산한 추정치와의 차가 되는 것이다. 이 차 y1
- ý1
은 a1, a2, ..., a10 에 대해서,
가정한 값의 잘못 등을 포함하고 있다. 만약 a1, a2, ...,
a10 의 설정이 적절하다면 영업소마다 계산한 y1
- ý1
은 작은 값이 될 것이다. 따라서 이와 같은 계산을 No.2 이하의 영업소에
대해서도 하게 되는데, 실제의 계산은 식 (1.3 ) 에서 m을 뺀 식을 계산한다
( 여기서 m은 식 (1.1)에서 사용되는 한개의 상수 즉 동일한 값임에 유의하라)
그 경우의 y1 -
ý1 에는
a1, a2, ..., a10 의 가정에 대한 잘못 외에 X1,
X2, …, X10 이외에 사용된 시간도 포함되게 된다.
그런데 미지수 a1, a2, ..., a10 에 대해서 3가지씩의 가정이 있으면 그 모든 조합은 310 = 59,049 가지이다. 이같은 방대한 조합수의 계산은 엄청난 것이며, 또한 그렇게 할 필요도 없으므로, 그 중에서 선택된 36가지의 조합에 대해서 계산한다. 어느 조합을 선택하는가는 직교표 (제2편 상론 3장 직교표 참조)에 따라 결정된다. 직교표는 실험의 능률화 등의 목적으로 실험계획법에서 자주 이용하고 있다. < 表 1.3 > 에서 보이는 것이 L36 직교표이며, 회귀분석의 미지수(실험에서의 인자) 13 개까지를 cover할 수 있다.
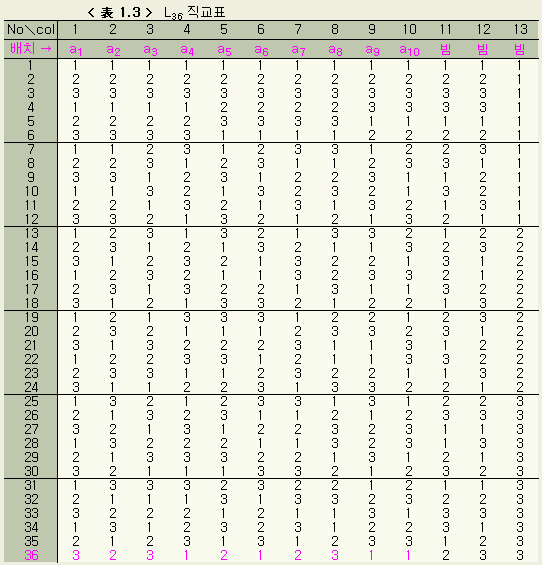
< 表 1.3 > 에서 col(umn)란의 숫자는 미지수의 종류를 나타내며, 표안의 숫자(1, 2, 3 으로만 표기된)는 그 미지수의 수준번호를 나타내고 있다. No.란은 수준 조합의 종류를 나타내고 있으므로, L36 의 경우 36 가지의 조합 내용이 표안의 숫자로 알 수 있게 되는 것이다.
10 개의 미지수 a1,
a2, ..., a10 을 제 1열~ 제 10열까지 차례로 대응시키고,
나머지 세열은 비워둔다. 예로서 마지막 No.
36 실험 조건이란
a1 은
제 3수준
a13 = 8.0
(분) (< 表 1.2 > 에서 설정된 수준별 값 )
a2 은
제 2수준
a22 = 4.0
(분)
a3 은
제 3수준
a33 = 8.0
(분)
a4 은
제 1수준
a41 = 0.0
(분)
a5 은
제 2수준
a52 = 4.0
(분)
a6 은
제 1수준
a61 = 0.0
(분)
............
a10 은
제 1수준
a101 = 0.0
(분)
으로 실험(계산)한다는 것을 나타낸다. 이 직교표에 실제 수준값을 넣은
것이 아래의 것이다.
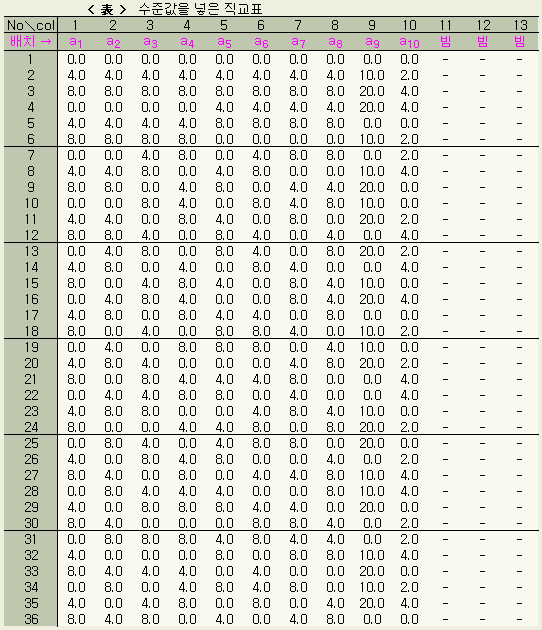
따라서 앞에서 설명한
작업분석의 경우, 36가지의 식
No.
1 ý = m + 0.0 X1
+ 0.0 X2 + ...
+ 0.0 X10
No. 2 ý
= m + 4.0 X1 +
4.0 X2 +
... +
2.0 X10
............
No. 36 ý
= m + 8.0 X1 +
4.0 X2 +
... +
0.0 X10
을
구성하고, 식의 우변에 각각 23 組의 X1, X2, ..., X10 의
값을 대입하여 실제의 작업시간 y 와의 차
를 계산한다.
즉 No. 1의
경우
y
- ( 0.0 X1 +
0.0 X2 +
... +
0.0 X10 )
= (m +) ε (1.4
)
즉 No. 1식에서
23組의 값을 대입하여 ε1,
ε2,
..., ε23 등
23개의 ε가 구해진다.
(No. 1, No. 2, ..., No. 36의 각각에 23조의 데이터를 대입하면, 즉 36 × 23 = 828회의 계산이 필요하다. 아래의 matrix형태로 된표의 노랑색 칸이 계산되어야 하는 ε 이다. 이런 계산은 엑셀이 제격이다)
|
|
|
|
|
|
|
|
|
|
|
X1 |
227 |
217 |
127 |
|
|
164 |
342 |
|
|
|
|
|
|
|
|
|
|
|
|
|
X2 |
94 |
100 |
133 |
|
|
55 |
47 |
|
|
|
|
|
|
|
|
|
|
|
|
|
X3 |
13 |
30 |
69 |
|
|
6 |
29 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
20.0 |
20.0 |
20.0 |
20.0 |
20.0 |
20.0 |
20.0 |
20.0 |
20.0 |
|
1674 |
1674 |
1674 |
1674 |
1674 |
1674 |
1674 |
1674 |
1674 |
|
|
|
|
|
|
|
|
|
|
|
X9 |
8 |
6 |
3 |
|
|
5 |
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
X10 |
70 |
41 |
36 |
|
|
39 |
84 |
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
1674 |
2131 |
2156 |
|
|
1694 |
2212 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
|
|
22 |
23 |
|
|
|
No. |
a1 |
a2 |
a3 |
|
a9 |
a10 |
빔 |
빔 |
빔 |
|
|
|
|||||||
|
|
1 |
2 |
3 |
|
9 |
10 |
11 |
12 |
13 |
|
T |
S |
|||||||
|
1 |
0 |
0 |
0 |
|
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
||
|
2 |
4.0 |
4.0 |
4.0 |
|
10.0 |
2.0 |
|
|
|
|
|
|
|
|
|
|
|
||
|
3 |
8.0 |
8.0 |
8.0 |
|
20.0 |
4.0 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
34 |
0 |
8.0 |
0 |
|
10.0 |
2.0 |
|
|
|
|
|
|
|
|
|
|
|
||
|
35 |
4.0 |
0 |
4.0 |
|
20.0 |
4.0 |
|
|
|
|
-172 |
|
|
|
|
|
|
||
|
36 |
8.0 |
4.0 |
8.0 |
|
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
||
35행의 제3열의 값(-172
)의 계산은
ε3
= 2156 - (4.0 × 127 + 0 *133 + 4.0 × 69 +
... +
20.0 × 3 + 4.0 × 36 )
=
-172
각
실험 No. 별로 ε1,
ε2,
..., ε23 의
합계를 T, 평균을 ε,
변동을 S로 하면, T, S는 다음의 식으로 나타낼 수 있다.
T
= ε1
+ ε2
+ ... + ε23
(1.5
) (※)
S =
( ε1 -
ε
)2 +
( ε2 -
ε
)2 +
... + ( ε23 -
ε
)2
=
ε12
+ ε22
+ ... + ε232
- T2
/ 23 (1.6
) (※)
36
가지에 대한 T, S 를 구하면 < 表 1.4 >로 정리될 수 있다.
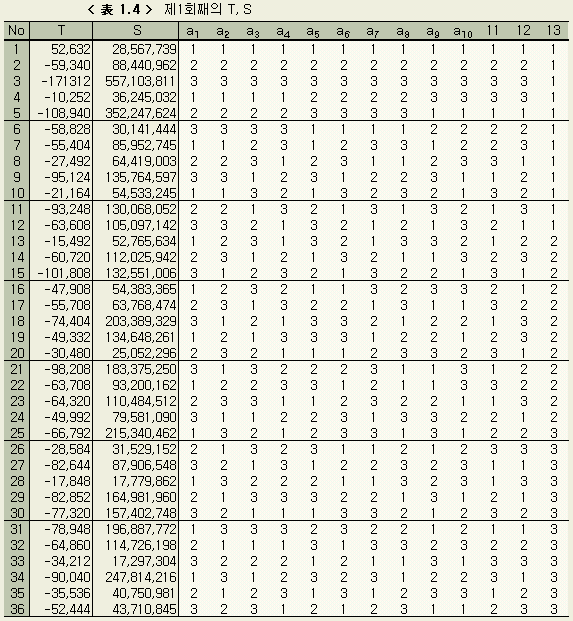
변동 S는 ε1, ε2, ..., ε23 의 변화의 크기(산포)를 나타낸다. 따라서 36 가지 식 중에서 가장 잘 들어맞는 식이 있다면, 그 식에서 23 개의 ε1, ε2, ..., ε23 의 값들은 비슷한 값이 될 것이고, 변동 S의 값은 작게 될 것이다.
그런데 미지수 a1의 경우, a11 = 0.0 (분), a12 = 4.0 (분), a13 = 8.0 (분) 의 3수준을 가정했지만 그 중에서 어느것이 좋은가를 보기위해서는 36 가지 중에서 a1을 제1수준의 0.0 (분)으로 계산한 No. 1, No. 4, No. 7, No. 10, ..., No. 34 의 12 개의 S의 값을 합한다. a1의 제2수준, 제3수준에 대해서도 마찬가지로 계산한다.
a11
의 S의 합 = 28,567,739 + 36,245,032 + ... + 247,814,216 = 1,218,118,494
a12
의 S의 합 = 88,440,962 + 352,247,624 +... + 40,750,981 = 1,298,495,156
a13 의 S의 합 = 1,733,321,114
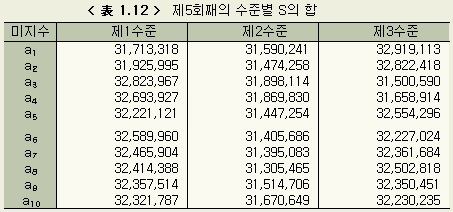
다른 미지수에 대해서도 마찬가지로 계산하면 < 表 1.5 > 가 얻어진다.
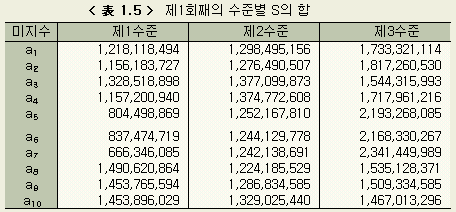
각 미지수에 대하여 3수준 사이의 S의 비교를 한다. 3수준 사이의 S의 값이 같은 정도라면, 가정한 3수준의 어느것을 계수 a로 하더라도 오차의 크기가 같아지게 된다. 그러나 만약 어느 한 수준의 S가 매우 작고, 나머지 두 수준의 S가 큰 경우에는 계수 a의 적절한 값은 S값이 작게 나타난 수준의 설정값 가까이에 존재하고 있다는 것을 암시하고 있으므로, 그 수준의 근방에서 더 좁은 폭의 3수준을 재 설정하여, 지금까지 설명한 계산을 되풀이해 간다.
실제로 < 表 1.5
> 의 결과에서 다음에 어떤 수단을 쓸것인가 하는 것은 다음과 같은 有意差
檢定에 의해서 결정되어진다 (어떤 미지수의 수준별로 차이가 인정된다
아니다를 각자의 주관, 감각적으로 판단해서는 안되는 법) 예를 들면 a11
과 a12 의 검정에는 다음의 분산비
F0
을 사용한다
F0
= (1 / 12 ) ×|S
(a11) - S (a12)|/
Ve
(1.7
) (※)
=
(1
/ 12 ) ×|1,218,118,494
- 1,298,495,156|/
40,442
=
66.98
여기서 Ve = 40,442 는 최소제곱법의 오차분산 Ve (엑셀에서 계산된, '잔차'의 '제곱평균') 이다. 최소제곱법으로 얻어지는 회귀계수는 신용될 수 없어도 오차분산은 믿을 수 있다. 분산비가 어느 값 이상이라면 비교한 수준간에 유의차가 있다고 할 것인가라는 명확한 기준은 없지만, 일반적으로 F0 가 2~4 이상이라면 有意差가 있다고 판정해도 실용상 문제는 없다 (분산분석에서 위험율 5 %, 1 %등으로 명확한 값이 계산되지만, 여기서는 그렇게 복잡 엄밀할 필요가 없다). 지금의 경우는 계산치가 66.98 이므로 a11 과 a12 의 사이에는 유의한 차가 있는 것으로 된다. S(a13)는 S(a12) 보다 더 큰 값이므로 a11 과 a13 간에도 당연히 유의차가 있다. 즉 S(a11)은 분명히 작은 값이라 할 수 있고, 따라서 미지수 a1을 지금 0.0 (분), 4.0 (분), 8.0 (분)의 세가지로 가정했지만, a11 = 0.0 (분)이 a12 = 4.0 (분)이나 a13 = 8.0 (분)보다 타당한 값에 가까이 있다고 볼수 있고, 따라서 다음의 계산에서는 a11주위의 더 좁은 폭의 3수준을 설정해야 하는 것이다.
3수준간의 유의차 검정은 3수준의 변동의 대소관계에 따라 다음과 같이 하는 것이 좋다. 3수준의 변동의 대소관계에는 6가지의 패턴이 있다. 각 패턴마다의 검정과 새로운 수준의 설정 방법은 < 表 1.6 > 과 같다.
| 패턴 | 변동 S의 대소관계 | 유의차의 상황 |
새 수준 |
||
|
1' |
2' |
3' |
|||
|
Ⅰ |
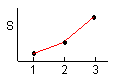 |
① 3수준간에 유의차 없음 |
1 1 0.5 (1) |
2 1.5 1 (1.5) |
3 2 1.5 (2) |
|
Ⅱ |
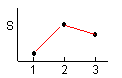 |
유의차 유무에 관계없이 | 1 | 2 | 3 |
|
Ⅲ |
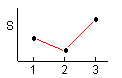 |
① 3수준간에 유의차 없음 |
1 1 1.5 |
2 1.5 2 |
3 2 2.5 |
|
Ⅳ |
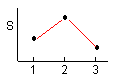 |
유의차 유무에 관계없이 | 1 | 2 | 3 |
|
Ⅴ |
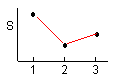 |
① 3수준간에 유의차 없음 |
1 2 1.5 |
2 2.5 2 |
3 3 2.5 |
|
Ⅵ |
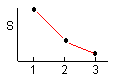 |
① 3수준간에 유의차 없음 |
1 2 2.5 (2) |
2 2.5 3 (2.5) |
3 3 3.5 (3) |
(
註 1 ) 위의 각 항에서 ②
③ 의 경우, 기울기가 급한 다른 쪽은 유의차 있음이란 의미이다.
( 註 2 ) 제1회째는
( )의 수준값,
제2회째 이후도 새로운 수준값이 초기의
설정범위 (한계치로 설정했음에 유의)를 벗어나는 경우는 ( )의
수준값을 택한다.
( 註 3 ) 1, 2, 3은
앞 단계에서의 수준값을 의미한다.
미지수 a1 의
경우, < 表 1.6 > 의 패턴Ⅰ의 ③에 상당하지만 1' = 0.5, 2'
= 1.0, 3' = 1.5 라는 식으로 하면 당초의 설정범위를 벗어나게 된다. 따라서
( )의 값을 취한다. 이것은 a11 = 1회째의 제1수준
= 0.0 (분), a12 = 제1과 제2수준의 중간 (表 1.6 에서는 1.5 로
표시) = 2.0 (분), a13 = 1회째의 제2수준 = 4.0 (분)으로 설정하는
것을 의미한다. (더 상세한 설명) a2,
a3, ..., a10 에 대해서도 마찬가지로 제2회째의 각 3수준
값을 설정한 것이 < 表 1.7 > 이다.
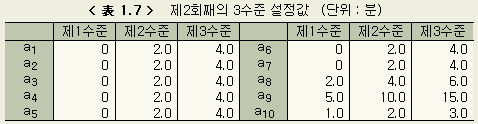
새로 설정된 수준에 따라, 제1회째와 마찬가지로 36가지에 대해서 23 개의 ε1, ε2, ..., ε23 을 계산한다. 합계 T, 변동 S, 수준별 S의 합을 < 表 1.8 >, < 表 1.9 > 에 보인다.
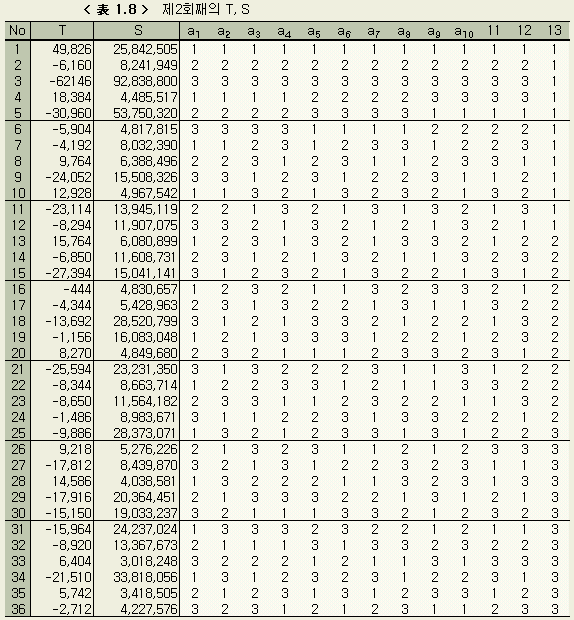
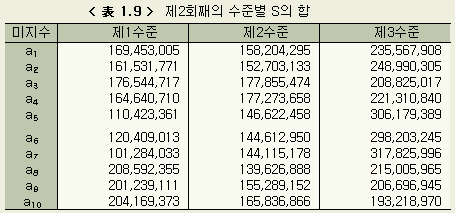
제1회째의 결과와 비교하면 각 변동(S)이 한자리 작아졌음을 알 수 있다. 이것은 제2회째의 각 3수준의 값이 더 타당한 쪽임을 보이는 것이다. 여기서 다시 유의차 검정을 하고, 3수준값을 정하여 제3회째의 계산을 한다. 이것을 모든 미지수에 대하여 3수준간에 유의한 차가 없어질 때 까지(收束이라고 한다) 반복한다. 단, 본디의 데이터에 자리수 착오의 잘못이 있거나, 미지수의 설정범위가 잘못된 경우에는 수속이 잘 되지 않는다. 이를 막기 위해서는 12회까지에서도 수속이 되지않을 경우 계산을 스톱시킬 필요가 있다. 큰 잘못이 없는 한, 대부분의 경우 6회 전후의 반복에서 수속된다. 이 예의 경우에서는 제5회째의 계산에서 a1, a2, ..., a10 의 각 수준간에 유의차가 없어졌다. 제5회째의 결과를 < 表 1.10 > ~ < 表 1.12 > 에 정리하였다.
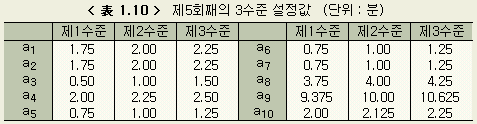
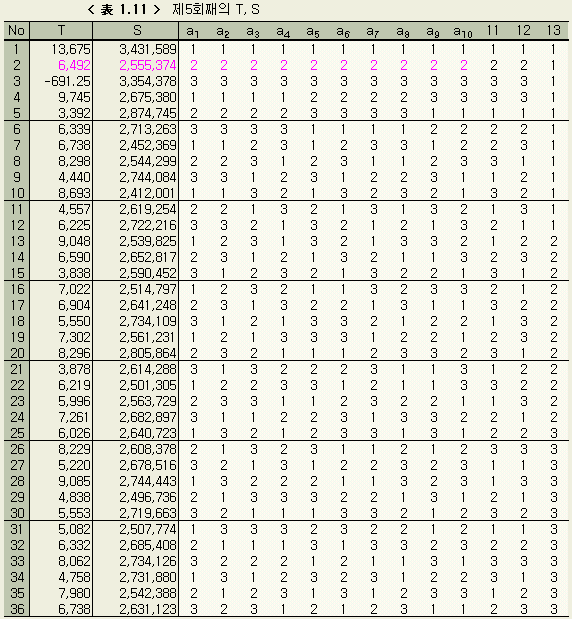
제5회째에서 모든
미지수의 3수준간에 유의차가 없어졌으므로, a1, a2, ...,
a10 은 < 表 1.10 > 에서 선정한다. 예를 들면 a1 에
대해서는 1.75 분에서 2.25 분 사이의 어떤 값이라도 job 1 의 단위시간으로 생각해도
좋다는 것이다. 여기서는 a1, a2, ..., a10 을
제5회째의 제2수준값으로 하는 것으로 한다. 즉
a1
= 1.75 ( ± 0.25 ) 分
a2
= 2.0 ( ± 0.25 ) 分
a3
= 1.0 ( ± 0.50 ) 分
......
a10
= 2.1 ( ± 0.10 ) 分
a1, a2,
..., a10 을 이와 같이 정하면 m 의 값은 < 表 1.11 >의 No. 2
의 T 의 값을 23 으로 나누면 얻어진다 (No. 2 의 조건은 모두 제2수준임을
주목하라. 식 (1.5 ) 에서
T = ε1
+ ε2
+ ... + ε23
).
m = T / 23
= 6,492
/
23 = 282.3
L36의
36가지 조합에도 없는 조합으로 a1, a2, ..., a10
이 선정될 때의 m 의 계산은 다음과
같이한다.
m = y
- ( a1X1
+ a2X2
+ … + a10X10
) 색상으로
평균을 표시함 (1.8
)
(
단, 평균은 < 표 1.1 >자료에서 구하는 값이다 )
여기서는 a1,
a2, ..., a10 의 값으로서 제5회째의 제2수준의 값을 택하는
것으로 하면 회귀식은 다음과 같이 된다.
y
= 282.3 + 1.75 X1 + 2.0 X2 + 1.0 X3
+ 2.2 X4 + 1.0 X5 + 1.0 X6
+
1.0 X7 + 4.0 X8 + 10.0 X9 + 2.1
X10 (1.9
)
식
(1.9 ) 의 오차분산은 < 表 1.11 >의
No. 2 의 S의 값을 써서 구할 수 있다. 즉
Ve
= Se / ( n - 1 )
=
2,555,374
/
22 = 116,153
이다.
이 값은 최소제곱법의 오차분산 40,442보다 크지만, 식 (1.9 ) 의 계수에 대한 모순을
포함하지 않으므로 실용적이다. 단 이 예제의 경우 설명의 편의상 데이터수를 줄였기
때문에(실제 조사에서는 X1, X2, …, X10 의
10가지 업무보다 더 많았다는 뜻) 계수 상호의 관계에서 약간의 모순이 있을지도
모르지만, 방법의 설명으로 이해해주시기 바란다.
精度좋은 미지수의 추정을 위해서는 이런 문제에서, 데이터의 개수가 적어도 50 개 이상이 바람직하다. 또 데이터 선택에서 사무량 Xi 가 비슷한 영업소만을 선정하지 말고, 모든 규모의 영업소로 부터 선택해야 할 것이다. 작업의 종류에서 극단적으로 양이 다를 경우에는 그 작업에 대해서 기계화된 경우도 있다. 즉 그 작업이 극단적으로 많은 곳과 그렇지 않은 곳은, 같은 작업이라도 작업내용이 다르기 때문에 그 표준시간도 달라진다. 그럴 때에는 하나의 작업을 두종류로 생각하여, 한쪽이 手작업, 다른 쪽이 기계에 의한 경우와 같이 표준시간을 두개로 나누는 것이다. 그 경우, 수작업으로 하는 영업소에서는 기계에 의한 작업건수를 0, 기계화되어있는 영업소에서는 수작업의 작업건수를 0으로 계산하는 것이다.
이상이 실험적 회귀분석의 개요이다. 이것은 달리 말하면 많은 미지수를 한목에 취하는 축차근사법이다.
최소제곱법으로 구한
식과 실험적 회귀분석으로 구한 식을 다시 써 보자.
(최소) y
= - 35.2 - 1.2 X1 + 2.0 X2 + 11.2 X3 +
12.7 X4 + 1.3 X5 + 0.7 X6
-
1.7 X7 - 22.6 X8 + 20.4 X9 - 3.0
X10 (1.10
)
(실험적) y
= 338.39 + 1.75 X1 +
2.0 X2 + 1.0 X3 + 2.2 X4 + 1.0 X5
+ 1.0 X6
+
1.0 X7 + 4.0 X8 + 10.0 X9 + 2.1
X10 (1.11
)
양자의 어느쪽이 좋은가를 판단할 때에, 통상 식의 오차분산을 비교하지만, 이 비교에는 최소제곱법이 좋은 것은 처음부터 명확하다 ( 최소제곱법은 미지수를 구할 때 사용하는 데이터와 구해진 미지수를 사용해 추정된 추정치와의 차의 제곱합이 최소가 되게 만들어지게 되는 까닭이다 ).
오차분산
외에 식의 良否의 판단척도로서 기여율이 있다. 기여율은 작업시간 y 의 변화의
몇 %를, X1, X2, …, X10
으로
표현하고 있는가를 나타내는 것으로 일반적으로 다음의 식으로 구한다. 지금 y 의
전변동을 ST,
식의 오차변동을 Se로
하면, 기여율 (%) 은
ρ
= ( 1 - Se
/
ST
)
× 100 (1.12
) (※)
이다.
그런데 y 의 전변동 ST
는
다음과 같다.
ST
=
( y1
- y )2
+ ( y2
- y )2
+ … + ( y23
- y )2
=
y1 2
+ y2
2
+ … + y23
2 - ( y1
+ y2
+ … + y23
)2 /
23 (1.13
) (※)
=
28,567,739
|
전변동
ST
(엑셀에서의 계산식) |
|
=devsq(데이터
혹은 그 범위) |
그래서
최소제곱법으로 얻은 식 (1.10 ) 의 기여율을 구해보면
ρ
= ( 1 - Se
/ ST
) ×
100
=
{ 1 - ( Ve
×
Ve의
자유도) / ST
} ×
100
=
1 - { 40,442 ×
( 23 - 10 - 1 ) } / 28,567,739
= 98.3 %
한편,
실험적 회귀분석으로 얻어진 식 (1.11 ) 의 기여율은 다음과 같이 된다.
ρ
= ( 1 - Se
/ ST
) ×
100 (1.14
)
=
1 - 2,555,374
/ 28,567,739
= 91.2 %
식
(1.14 ) 의 Se
는
< 表 1.11 >의 제5회째의 S난에서 구한다. 이 경우 10개의 계수로서
제2수준을 채용했으므로, No. 2 의 S 값 2,555,374
가 Se에
해당된다. 그런데 개개의 작업시간의 추정을 식 (1.10 ), 식 (1.11 )로 하면
어떻게 되는가를 보자. 23개소의 영업소의 X1,
X2, …, X10 을
식 (1.10 ) 와 식 (1.11 ) 에 대입해서 계산한 작업시간과 실제 측정한 값과의
차 및 제곱합(표의 끝)을 계산한 것이 < 표 1.13 > 이다.
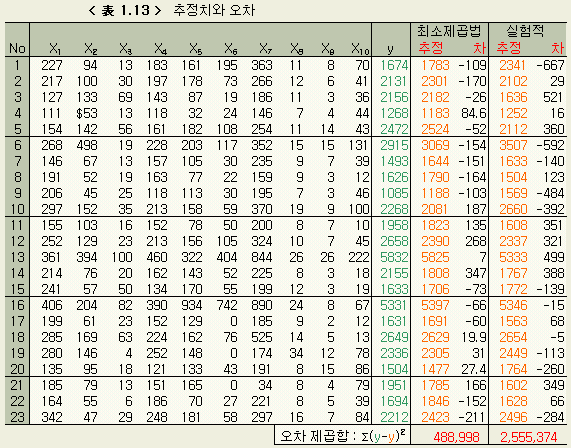
< 表 1.13 > 의 오차의 제곱합을 비교해 보면, 실험적 회귀분석으로 얻어진 식 (1.11 ) 의 것이 식 (1.10 ) 의 약 5배인 것을 볼수 있다.
그러면 여기서 식을 만들 때 사용한 23개소 이외의 데이터에 대해서 계산을 해보자. 23 개소 이외의 데이터로서 No. 24 부터 No. 35 까지의 12 개소의 데이터를 맞춰본 결과는 < 表 1.14 > 와 같다.
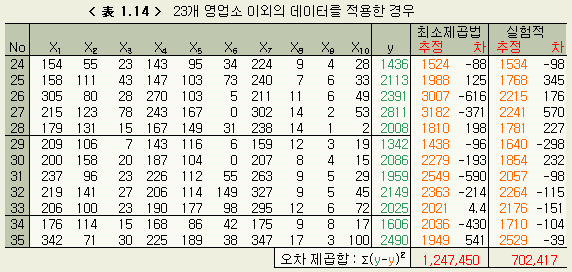
< 表 1.14 > 의 오차의 제곱합을 비교하면 놀라운 것은, 실험적 회귀분석의 경우가 최소제곱법의 약 半이라는 사실이다. 이것은 식의 좋고 나쁨을 식을 만들때의 (사용한 데이터의) 오차분산만으로 판단해서는 안된다는 것을 의미한다. 식을 만들 때 사용하지 않은 나머지 영업소 혹은 장래의 데이터에 대해서 잘 맞아떨어지는 것이 실제로 중요한 것이다. 그러므로 사내에서 이와 같은 방법으로 몇가지의 회귀식의 양부를 판단할 때에는 최초에 회귀식을 만들 때, 전부의 데이터를 사용하지 말고, 몇개의 데이터라도 남겨두어 나중에 확인하는것이 좋다. 특히 회귀식을 예측등에 이용할 때에는 이것이 중요하다.
이 예의 경우, 회귀식 작성에 사용하지 않은 데이터에 대해서의 오차의 제곱합은 실험적 회귀분석으로 얻은 식 (1.11 ) 의 쪽이 작았다. 이것만의 결과로 어떤 경우에도 실험적 회귀분석에 의한 쪽이 재현성이 좋은 것이라고 이해하는 것은 위험하지만, 실험적 회귀분석에 의한 회귀식의 계수의 타당성이 이와 같은 결과를 생기게 한 하나의 요인이라는 것은 쉽게 推察된다.
실험적
회귀분석으로 식의 계수를 축차적으로 구해갈 때, 가장 어려운 문제는 최초에 미지수의
범위를 어떻게 설정할 것인가이다. 계수가 단위당의 작업시간과 같은 경우는 비교적
쉬운 경우지만, 그렇더라도 너무 넓은 범위를 잡으면, 축차근사의 효율이 낮아진다.
그 점만으로도 참값으로 수속되지 않는 수도 있다. 이것은 마치 최적온도조건이 30
℃ 근방인데도, 0 ℃와 500 ℃와 1000 ℃로 실험해서 최적온도를 찾으려 해도 잘되지
않는 것과 같다. 최초로 설정한 범위내에서, 최적값이 포함될 것이 필요조건이기는
하지만, 충분조건은 아니다. 그러나 범위에 대해 전혀 감이 잡히지 않을 경우는
먼저 넓은 범위로 해보는 이외는 방법이 없겠다.
|
제5편 Simulation 2장 실험적 회귀분석의 기초 (데이터가 적거나 1차식이 아닌 경우) |
실험적
회귀분석에서 미지수를 구하는 방법의 특징의 하나는 검정과 축차근사를 반복한다는
점이다. 1章에서는 두 수준간의 유의차를 조사하는데, 다음의 분산비를 사용했다.
F0 =
(1 / 12 ) ×|S
(a11) - S (a12)|/
Ve (2.1)
이
계산에서 사용된 오차분산은 회귀분석을 최소제곱법으로 풀때의 오차분산 Ve
이다.
그런데 앞의 예에서 만약 데이터가 적을 때는 어떻게 되는가? 데이터의 수가 미지수의 개수보다 적을 경우에는 최소제곱법으로 풀 수 없다. 그러면 실험적 회귀분석의 경우는 어떻게 해야 하는가?
식 (2.1) 의 분산비의 계산에 필요한 Ve 로서, 최소제곱법으로 얻어지는 오차분산을 사용하려고 한다면, 실험적 회귀분석에서의 검정은 불가능하다. 그러나 분산비를 만들 때의 오차분산만 해결된다면, 실험적 회귀분석은 데이터의 수가 미지수의 그것보다 작아도 이용할 수 있게된다. 또 최소제곱법이 기술적으로 곤란한 문제, 예를 들면 함수가 미지수에 대해서 비선형의 경우등에도 실험적 회귀분석이 유효한 수단이 될 수 있을 것이다. 이 장에서는 이와같은 경우의 분산비의 계산에 사용되는 오차분산 Ve 의 취급법에 대한 하나의 방안을 제시한다. 먼저 1章의 데이터를 다시 실어 문제를 정리해보자.
지금
회사의 사무작업을 분석하려고 한다. 각 영업소의 주요한 작업은 10 種이지만
10 개 영업소의 작업건수 X1, X2, …, X10 과
그 날의 각 영업소에서의 작업시간 y 의 데이터가 < 表 2.1 > 이다.
(이 데이터는 1章의 23개 데이터중 처음 10 개이다)
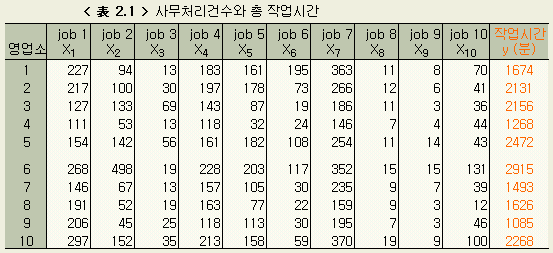
<
表 2.1 > 의 데이터에 대해, 1章과 같이 1차식을 상정해보자.
y =
m + a1X1 + a2X2 + … + a10X10
이
식에서 m, a1, a2, ..., a10 를 추정하는
것이 이 章의 문제이다.
회귀분석을 최소제곱법으로 풀때의 오차분산은, 같은 함수형으로 다른 어떤 값의 계수를 갖는 식보다 작은 값을 갖는다. 그런데 오차분산이 커지면 기여율은 작아진다. 바꿔말하면 최소제곱법으로 얻어진 식이 최고의 기여율을 나타낸다. 1章의 사무작업분석을 할 때 식 (1.12 )에서 나타낸 바와 같이 그 기여율은 98.3 %였다.
오차변동
Se
와 기여율 ρ,
전변동 ST
간에는 다음의
관계가 있다.
Se
= ( 1 - ρ /
100 ) ×
ST
(2.2
)
(※)
또
오차변동 Se
로부터 오차분산
Ve
를 구하는 데는 Se
를 그 자유도로
나누면 된다. 최소제곱법의 경우 데이터 개수가 n 이고, 미지수가 k 개이면,
그 자유도는 ( n - k -1 ) 이지만, 실험적 회귀분석의 경우는 ( n - 1 ) 로 해도
좋다.
구하려는
식이 대략 몇 % 정도의 기여율을 갖는가를 짐작한다면, 식 (2.2 ) 에서 오차변동
Se 가 정해지고,
다음 식으로 오차분산 Ve
가 계산된다.
Ve =
Se / ( n - 1 ) (2.3
)
최소제곱법을 풀 수 없어 오차분산을 결정할 수 없을 때, 이와같이 얻어지는 값을 검정에서 오차분산 Ve 에 대용하려는 것이 그 방안이다. 그렇기 위해서는 회귀관계의 기여율의 예상을 하는 것이 필요하다. 물론 그와같은 기여율의 예상을 정확히 한다는 것은 어렵고, 또 예상을 세운다 하더라도, 그에대한 확신이 없는 경우가 많다. 여기서는 예상한 기여율로서 산출한 오차분산으로 검정한 것이 타당한가의 여부의 판단으로서 다음과 같이 하는 것이다.
먼저
예상한 기여율로 계산한 오차분산을 써서 실험적 회귀분석을 진행시키고, 그 결과로
얻어진 회귀식의 기여율을 조사해본다. 얻어진 회귀식에서의 기여율과 처음
예상한 기여율 간에 큰 차가 있는 경우에는 예상 기여율에 문제가 있는 것이된다.
예를 들어 예상 기여율을 90 %로 해서 실험적 회귀분석을 진행시켰다고 하자. 즉
실험적 회귀분석의 검정에는 다음의 오차분산이 사용되는 것이 된다.
Ve =
Se / ( n - 1 )
=
{ ( 1 - ρ / 100 )
× ST
}
/ ( n - 1 ) (2.4
)
(※)
=
{ ( 1 - 90 / 100
) × ST
}
/ ( n - 1 )
=
{ 0.1 ×
ST
} /
( n - 1 )
그 결과 얻어진 식의 기여율이 90 % 보다 낮다면, 검정에 사용한 기여율을 과다하게 추정 ( 즉, 오차분산을 과소추정) 한 것이므로, 예상기여율 ρ를 90 %보다 낮게, 예를 들면 80 % 혹은 70 %로 해서 다시 회귀분석을 한다. 예상한 기여율과 얻어진 회귀식의 기여율이 거의 밸런스가 이뤄지는 것이 타당한 지점인 것이다. (엑셀을 사용하면 동일한 식에서 자동계산이 됨으로 큰 부담이 아니다)
여기서는
< 表 2.1 >의 데이터를 사용한다. 이 경우 예상기여율이 80 % 정도라고 생각되지만,
확신이 없으므로 일반적인 계산법으로 다음의 6가지에 대해 계산한다.
(1)
ρ= 98 % (오차의 기여율로 2 %)
(2)
ρ= 96 % (오차의 기여율로 4 %)
(3)
ρ= 92 % (오차의 기여율로 8 %)
(4)
ρ= 84 % (오차의 기여율로 16 %)
(5)
ρ= 68 % (오차의 기여율로 32 %)
(6)
ρ= 36 % (오차의 기여율로 64 %)
미지수의
범위는 1章의 경우와 같은 것을 사용한다.
2.3.1 예상기여율 ρ= 98 % 의 경우
먼저
전변동 ST
를 구해보자
ST
= 16742 + 21312 + 21562 + … +
22682 - ( 1674 + 2131 + 2156 + … + 2268 )2 / 10
=
39,401,580 - 19,0882 /10 = 2,966,406
따라서
ρ= 98 %의 경우 검정에 쓰일 오차분산 Ve
는 다음과 같이
구해진다
Ve
= { ( 1 - ρ /
100 ) × ST
} / ( n - 1)
=
{ ( 1 - 98 / 100 ) × 2,966,406 } / ( 10 - 1 )
=
ST 의
2 % / ( 10 - 1 )
=
6,592
이 오차분산을 사용하는 이외는 1章과 같은 방법의 실험적 회귀분석을 진행시킨다. 그 결과 제6회째에서 10 개의 미지수의 3수준간에 유의차가 없어졌다.

제6회째의 T, S 및 수준별의 S 의 합은 < 表 2.4 > < 表 2.5 > 와 같다.
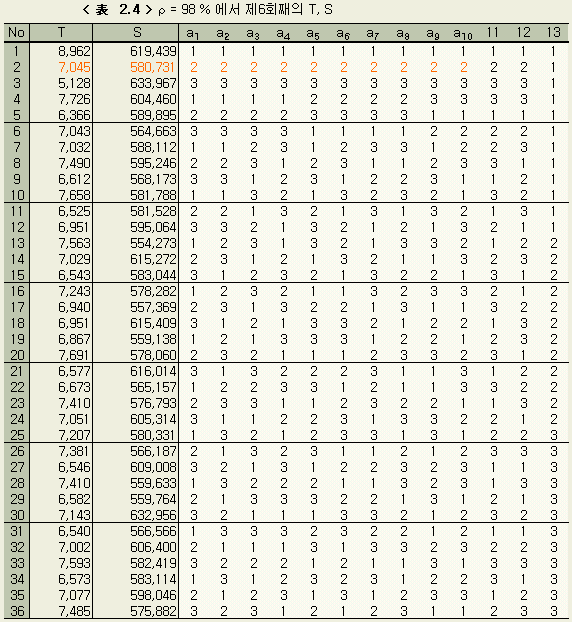
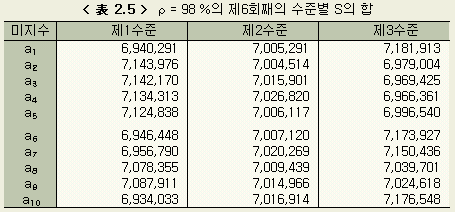
10개의
계수로서 < 表 2.3 >
의 제2수준을 써서 회귀식을 만들면 다음과 같다.
y =
m + a1X1 + a2X2 + … + a10X10
=
7,045 /
10 + 0.625 X1 + 1.625 X2 + … + 2.00 X10
이
경우 기여율은 다음과 같다.
ρ = ( 1 - Se
/
ST
)
× 100 (2.5
)
(※)
=
(1 -
580,731
/
2,966,406 ) × 100 = 80.4 %
예상기여율은 98 %였으므로, 회귀식의 80.4 %라는 결과로 볼 때, 이 실험적 회귀분석의 검정에 사용한 오차분산값은 너무 작게 잡은 것이다.
2.3.2 다른 예상기여율의 경우
회귀의
기여율 ρ= 96 %의 경우, 오차의 기여율은 4 %이다. 따라서 검정에 사용되는 오차분산의
크기는
Ve =
( 0.04 × 2,966,406 ) / 9 = 13,184
이것은, 앞절의 검정에 사용한 오차분산의 2배에 해당된다. 실험적 회귀분석은 이 경우, 제5회째에서 수속되었다. 이하 제5회째의 결과를 나타낸다. < 表 2.6 > 은 미지수의 범위이고, < 表 2.7 > 은 T, S < 表 2.8 > 은 수준별 S의 합이다.

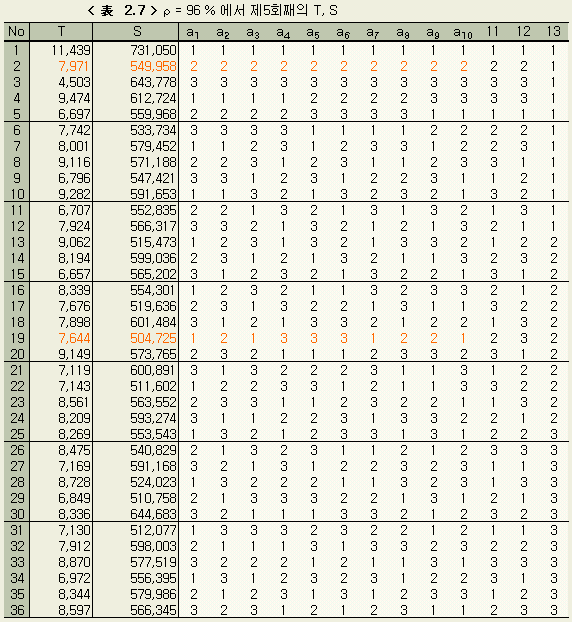

여기서도
10 개의 계수로서 < 表 2.6 >
의 제2수준을 취하면 식은 다음과 같이 된다.
y =
7,971 / 10 +
0.25 X1 + 1.75 X2 + … + 2.00 X10
(2.6
)
기여율
ρ 은
ρ =
(1 - Se
/
ST
)
× 100
=
(1 - 549,958
/
2,966,406 ) ×100
=
81.5 %
예상기여율은 지금의 경우, 96 %였으므로 양자간에는 아직 차가 보인다. 그러나 그 차는 앞 절의 경우보다 많이 줄어졌음을 알 수 있다.
식
(2.6)은 10개의 계수로서 < 表 2.6 >
의 제2수준을 취한 것이나, 그 외에도 유의차가 없는 식은 몇개라도 생각할 수 있다.
특히 최종단계의 3수준의 값중에 0 을 포함하고 있을 때에는, 0 을 채용함에 의해
변수를 제거할 수도 있다. 예를 들면 < 表 2.7 >
의 36가지 중에서 가장 S의 값이 작은 No.19 의 경우를 생각하면 회귀식은
다음과 같다.
y =
m + a11X1 + a2X2 + … + a10X10
=
m + a11 X1 + a22 X2 + a31 X3
+ a43 X4 + a53 X5 + a63
X6
+
a71 X7 + a82 X8 + a92 X9
+ a101 X10
y =
7,644 / 10 (+
0.0 X1)
+
1.75 X2
+ 4.5 X3
+ 2.0 X4
+ 1.5 X5 + 0.5
X6
(+
0.0 X7
) + 4.0 X8
+ 10.0 X9
+ 1.75 X10
(2.7
)
No
19 의 난으로 부터 Se =
504,725
이므로,
식 (2.7 ) 의 기여율은 다음과 같다
ρ =
(1 - 504,725
/
2,966,406 ) × 100
=
83.0 %
이것은
식 (2.6) 의 기여율 81.5 %와 비교해 큰 차이가 없는것같다. 그것은 양자 모두 실험적
회귀분석에 의해 유의차가 없어진 단계에서 선정된 조합인것을 생각하면 당연한 것이다.
다음에 예상기여율을 92 %, 84 %, 68 %, 36 %로 바꿔서 회귀분석을 한 결과를 나타낸다. 최종 단계(수준간에 유의차가 없이 수속된 단계) 에서의 각 미지수의 3수준값을 < 表 2.9 > 에, 최종단계의 T, S 의 表의 일부를 < 表 2.10 > ~ < 表 2.13 > 에 나타낸다.
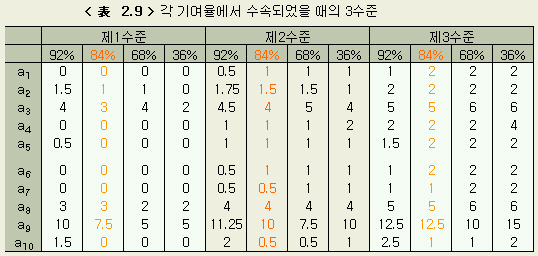
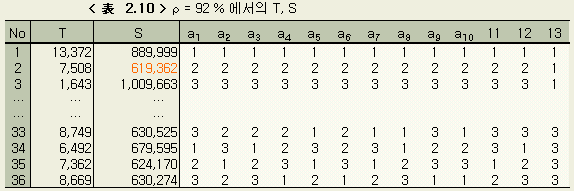
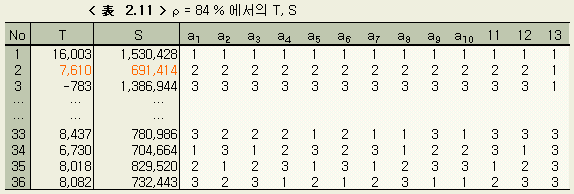
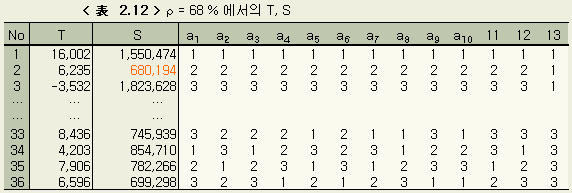
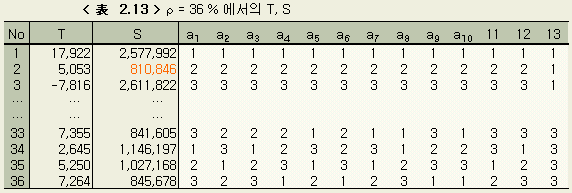
다음에 예상기여율을 몇 %로 설정할 때가 가장 타당한가를 보기위해, 각각의 경우의 회귀의 기여율을 앞절과 같은 방법으로 계산하여 < 表 2.14 > 에 나타낸다. 회귀식으로는 No. 2 의 값을 취했다.
< 表 2.14 > 에서 예상기여율을 84 % 즉, 검정의 오차분산 Ve 를 52,736 (이것은 전변동의 16 %에 해당된다)으로 했을 때가 가장 타당하다고 할 수 있다 ( 여기서 Ve = Se / ( n - 1 ) = Se / 9 )
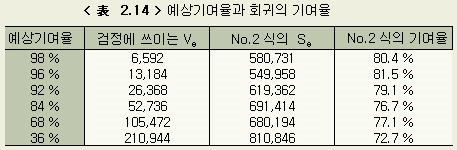
그런데 < 表 2.14 > 와 < 表 2.9 > 에서 검정에 사용한 오차분산이 달라도, 최종단계에서 미지수의 범위는, 오차분산이 크게 다른것 치고는 별로 다르지 않음을 본다. 따라서 이와 같은 실험적 회귀분석을 이용하는 경우, 예상기여율에 대해서 그만큼 엄밀하게 생각할 필요는 없음을 안다.
|
실제 계산 ( 계산의 直行 ) |
|
여기서는 설명을 위해 예상기여율을 98 %~36 % 등으로 계산결과를 보이지만, < 表 2.14 > 에서 기여율이 98 %~36 % 로 달라져도 No.2 의 Se값은 비슷한 값을 나타낸다. 그러므로, 처음 어떤(임의의) 기여율로 검정과 축차근사를 하여 5 ~ 6 단계로 수속되면, 그 때의 No. 2의 Se 값에서 Ve값을 계산하여 {Ve = Se / ( n - 1)}, 그 값이 < 表 2.14 > 의 좌반부에서 어느값에 가까운가를 찾아 예상기여율로 적용시킨다면 여기서와 같은 여러 단계의 기여율 적용계산을 생략할 수 있다. 이 예에서는 < 表 2.4 > No.2 의 Se가 대략 58 만이므로 Ve = 58 만 / (10 - 1) ≒ 6 ~ 7 만, 따라서 < 表 2.14 > 의 좌반부에서 84 %가 가장 근접한 값이다. 따라서 Ve는 52,736을 잡아 직행할 것이다. |
지금의
경우, 예상기여율 84 %의 결과를 사용하는 것으로 하면, 회귀식은 식 (2.8 ) 와 같이된다
y =
m + a11X1 + a2X2 + … + a10X10
=
7,610 /
10 +
1.0 X1 + 1.5 X2
+ 4.0 X3
+ 1.0 X4
+ 1.0 X5 + 1.0
X6
+
0.5 X7 + 4.0 X8
+ 10.0 X9
+ 0.5 X10
(2.8
)
회귀식 (2.8 ) 의 X1, X2, , …, X10 으로서 1章의 식 (1.10 ), 식 (1.11 ) 을 비교할 때 사용한 < 表 1.14 > 의 12組의 데이터를 사용해 최소제곱법과 비교해보자. 결과는 < 表 2.15 > 와 같다.
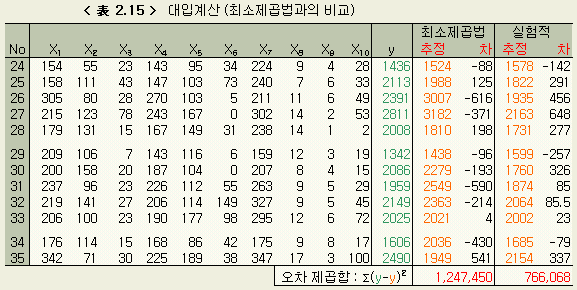
이 결과를 1章의 < 表 1.14 > 와 비교하면, 10組만의 데이터로 구한 회귀식은 23組의 그것보다 정도는 조금 나쁘지만, 최소제곱법의 결과보다는 좋은 것으로 나왔다.
이상으로 부터 사용할 데이터수가 미지수의 개수보다 적은 경우에는 (또는 1차식이 아닌 함수형의 경우에도), 결과의 타당성(精度)에서는 떨어지지만, 실험적 회귀분석에 의해 회귀식을 찾는 것이 가능하고 또한 실용적인 해법이 된다.